一文搞懂策略梯度(Policy gradient)算法(一)
《文明VI》是一款历史背景下的大型策略游戏,策略性丰富且耐玩。 #生活乐趣# #游戏乐趣# #策略游戏#
引言
在强化学习的过程中,从 Sarsa 到 Q-learning 再到 DQN,本质上都是值函数近似算法。
值函数近似算法都是先学习动作价值函数,然后根据估计的动作价值函数选择动作。如果没有动作价值函数的估计,策略也就不会存在。 例如,DQN的神经网络结构可以表示为如下图所示:
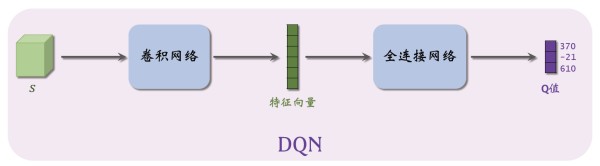
图中,输入是状态 s s s,输出是每个动作的 Q Q Q 值,即对每个动作的评分,分数越高意味着动作越好。通过对值函数的近似,我们可以知道回报最大的路径,从而指导智能体进行动作的选取。
但是,强化学习的目标,是学习最优策略。那么有没有一种可能,我们可以跳过动作价值的评估环节,直接从输入状态,到输出策略呢?
——策略梯度算法
在策略梯度算法中,策略函数的输入是状态 s s s 和动作 a a a,输出是一个0到1之间的概率值,当前最有效的方法是用神经网络近似策略函数。给出一个策略网络结构图:
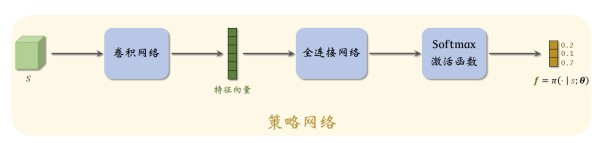
如图,在策略网络结构中,输入是状态 s s s,输出是动作空间中每个动作的概率值。
两个关键
现在我们已经有了想法——直接从输入得到最优策略,那么随之而来
两个问题:
1、如何来衡量一个策略的好与坏?
2、如何搜索最优策略?
先来看看《强化学习》中关于策略梯度算法的定义:
策略梯度方法基于某种性能度量 J ( θ ) J(\theta) J(θ) 的梯度,这些梯度是标量 J ( θ ) J(\theta) J(θ) 对策略参数的梯度。这些方法的目标是最大化性能指标,所以它们的更新近似于 J J J 的梯度上升
梯度上升: θ t + 1 = θ t + α ∇ J ( θ t ) ^ \theta_{t+1}=\theta_t+\alpha\widehat{\nabla{J(\theta_t)}} θt+1=θt+α∇J(θt)
其中, ∇ J ( θ t ) ^ \widehat{\nabla{J(\theta_t)}} ∇J(θt)
是一个随机估计,它的期望是性能指标对它的参数 θ t \theta_t θt 的梯度的近似。我们将所有符合这个框架的方法都称为梯度策略法。
解决思路:
1、使用一个目标函数定义最优策略;
2、基于梯度的优化算法;
下面我们分别论述这两个关键点。
目标函数
从上文中定义可以看出,策略梯度方法的目标函数即为某种性能度量 J ( θ ) J(\theta) J(θ) , 策略可以用任意的方式参数化,只要 π ( a ∣ s , θ ) \pi(a|s,\theta) π(a∣s,θ) 对参数可导。
平均状态价值
由状态价值的定义
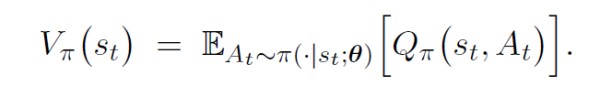
可以看到,状态价值即依赖当前状态 s t s_t st,也依赖于策略网络 π \pi π 的参数 θ \theta θ,进行说明:

如果一个策略很好,那么其状态价值 V π ( S ) V_{\pi}(S) Vπ(S) 的均值应当很大。因此定义目标函数
J ( θ ) = E S [ V π ( S ) ] J(\theta)=E_S[V_\pi(S)] J(θ)=ES[Vπ(S)]
为啥这样定义呢?
其实前面说了, V π ( S ) V_{\pi}(S) Vπ(S) 依赖于当前状态和策略网络,因此对状态进行期望操作得到目标函数 J ( θ ) J(\theta) J(θ),这样 J ( θ ) J(\theta) J(θ) 就只依赖于策略网络 π \pi π 的参数 θ \theta θ——策略越好,则 J ( θ ) J(\theta) J(θ) 越大。
即,策略学习可以描述为优化问题: m a x J ( θ ) max J(\theta) maxJ(θ)
上述定义的目标函数中,设 d ( s ) d(s) d(s) 为状态 s s s 的权重,有

则对于 d ( s ) d(s) d(s) 而言,分为两种情况:
1) d d d 独立于策略 π \pi π

2) d d d 依赖于策略 π \pi π

主要的区别,就在于求梯度的时候,计算有所不同。
平均奖励
第二种度量最优策略的目标函数为平均奖励,此处给出定义,不过多阐述。

结合以上,有策略梯度算法的基本思想:
1、所有的目标函数都是关于策略 π \pi π 的方程;
2、策略 π \pi π 由 θ \theta θ 参数化,因此所有的目标函数是关于 θ \theta θ 的方程;
3、不同的 θ \theta θ 生成不同的目标函数值;
4、通过搜索 θ \theta θ 的最优值最大化目标函数。
策略梯度
此处以王树森 ——《深度强化学习》为基础,对策略梯度定理的简要证明进行阐述。
首先,回顾以下状态价值函数的定义:
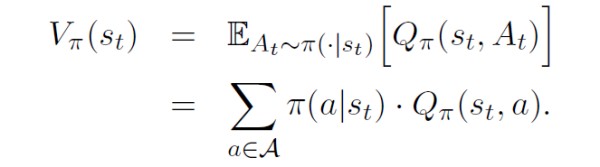
基于神经网络近似的策略函数中,将策略网络 π ( a ∣ s ; θ ) \pi(a|s;\theta) π(a∣s;θ) 看作动作的概率质量函数(或概率密度函数)。则状态价值 V π ( s ) V_\pi(s) Vπ(s) 可以写成:
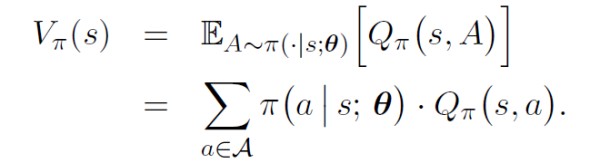
状态价值函数关于 θ \theta θ 的梯度可以写作:

由链式法则,有

上式最右面一项 x x x 的分析非常复杂,此处不具体进行分析。可得

进行替换,则有
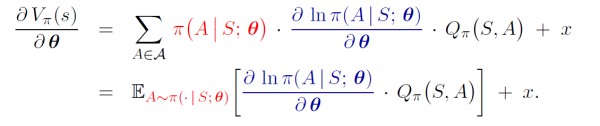
由目标函数的定义,得

以上。
简要证明到此结束,问题来了。
这个公式,好像不能直接用?
为啥?
策略梯度的求解过程中,需要知道两个东西,一个是状态 S S S 的概率密度函数 π ( A ∣ S ; θ ) \pi(A|S;\theta) π(A∣S;θ),另一个是动作价值函数 Q π ( S , A ) Q_{\pi}(S,A) Qπ(S,A)。
先来看 π ( A ∣ S ; θ ) \pi(A|S;\theta) π(A∣S;θ),如果我们知道所有状态的分布信息,那么求期望是可行的,但是很显然,我们并不知道状态 S S S 的概率密度函数;即使我们知道,能够通过连加或者定积分求出期望,我们也不愿意这么做,因为连加或者定积分的计算量非常大。
怎么办呢?——这里用到了随机近似的概念。
每次从环境中观测到一个状态 s s s ,相当于随机变量 S S S 的观测值。然后再根据当前的策略网络(策略网络的参数必须是最新的)随机抽样得出一个动作:
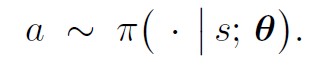
计算随机梯度:

则有:
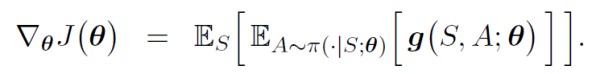
但是,但是,但是
动作价值函数 Q π ( S , A ) Q_{\pi}(S,A) Qπ(S,A),我们也不晓得啊!~
基于之前学到的值函数近似算法,我们有两种方法可以得到价值函数 Q π ( S , A ) Q_{\pi}(S,A) Qπ(S,A)。
1、蒙特卡洛;
使用实际观测的回报 u u u 近似 Q π ( S , A ) Q_{\pi}(S,A) Qπ(S,A),这种方法被称为——REINFORCE。
2、TD算法;
使用神经网络 q ( s , a ; w ) q(s,a;w) q(s,a;w) 近似 Q π ( S , A ) Q_{\pi}(S,A) Qπ(S,A),这种方法被称为——actor-critic。
结束
关于 REINFORCE 和 actor-critic,后续有机会再介绍。
到此为止,就算是完成了策略梯度(PG)算法的简要介绍,希望能帮到各位理清算法脉络。
参考资料
王树森——深度强化学习
赵世钰——强化学习的数学原理
Richard S. Sutton——强化学习
网址:一文搞懂策略梯度(Policy gradient)算法(一) https://www.yuejiaxmz.com/news/view/548799
相关内容
强化学习(三)—— 策略学习(Policy创建高性能强化学习环境:关键技术与优化策略
【机器学习算法】梯度提升方法
一文搞懂策略模式(优化策略模式完全消除if else)
常见的几种最优化方法(梯度下降法、牛顿法、拟牛顿法、共轭梯度法等)
优化算法综述
一文了解强化学习
最速下降法入门:算法原理与应用
RL笔记:动态规划(1): 策略估计和策略提升
强化学习下的无人驾驶决策技术

