x i θ = e i ∗ l n ( x θ ) ( 向 量 ( 1 , 0 ) 从 0 转 到 l n ( x θ ) ( 弧 度 制 ) ) x ^{i θ}=e^{i*ln(x^θ )}(向量(1,0)从0转到ln(x^θ)(弧度制)) xiθ=ei∗ln(xθ)(向量(1,0)从0转到ln(xθ)(弧度制))
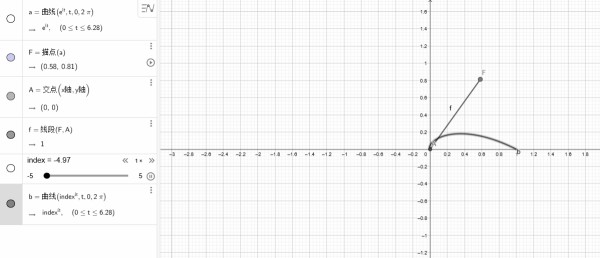
在 x ∈ [ 0 , 2 π ] , 底 数 a ≥ e 时 , 才 能 形 成 整 个 圆 周 在x\in[0,2\pi],底数a \geq e时,才能形成整个圆周 在x∈[0,2π],底数a≥e时,才能形成整个圆周
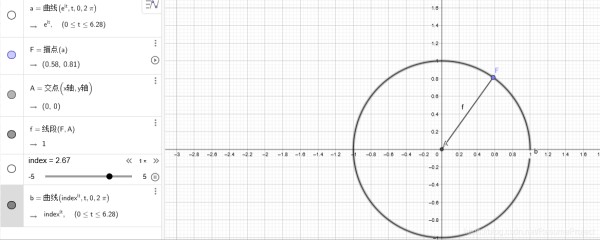
底 数 为 e 时 , 在 x ∈ [ 0 , 2 π ] , 正 好 就 是 一 个 圆 周 底数为e时,在x\in[0,2\pi],正好就是一个圆周 底数为e时,在x∈[0,2π],正好就是一个圆周
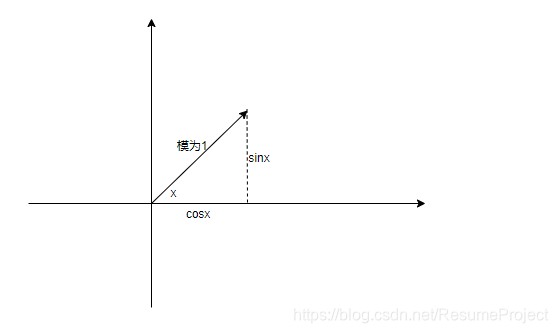
e i x = c o x x + i s i n x e^{ix}=coxx+isinx eix=coxx+isinx
https://krasjet.github.io/quaternion/quaternion.pdf
https://github.com/Krasjet/quaternion




