强化学习笔记二

发布时间：2024-11-20 02:56

学会整理笔记，强化记忆 #生活技巧# #学习技巧# #考试复习技巧#

Reinforcement Learning学习笔记

Lecture 2

笔记基于David Silver 的上课内容及PPT。
视频地址（B站中文字幕）：https://www.bilibili.com/video/av9833386
PPT地址：http://101.96.10.63/www0.cs.ucl.ac.uk/staff/d.silver/web/Teaching_files/MDP.pdf

Markov Process

Introduction

马尔科夫决策过程可以很好地表示强化学习的环境，环境的状态是完全可以监控感知的。几乎所有的强化学习的可以被形式化的转换为MDP。马尔科夫决策过程中最重要的就是每一个状态都要符合马尔科夫性质，也就是未来的状态只与现在的状态有关，是独立于过去的所有状态的：P [St+1 | St] = P [St+1 | S1, …, St]，也就是这个状态是对历史所有信息的统计。

对于一个具有马尔科夫性质的s和下一个状态s’，可以定义从s转移到s’的概率为

p s s ′ = P [ S t + 1 = s ′ ∣ S t = s ] p_{ss'}=P[S_{t+1} = s'| S_t = s] pss′=P[St+1=s′∣St=s]

状态转移矩阵P定义了所有状态s到可能的后继状态s’的转移概率：
t o to to

P = f r o m [ P 11 ⋯ P 1 n ⋮ P n 1 ⋯ P n n ] P= from \left[

P11amp;⋯amp;P1n⋮amp;amp;Pn1amp;⋯amp;Pnn" role="presentation">P11amp;⋯amp;P1n⋮amp;amp;Pn1amp;⋯amp;Pnn

\right] P=from⎣⎢⎡P11⋮Pn1⋯⋯P1nPnn⎦⎥⎤
因为矩阵的每一行都代表的当前状态转移到下一状态的概率，所以每一行的概率和都为1。

Markov Chains

基本上，一个Markov Process，马尔科夫过程是一个随机过程，也就是由具有马尔科夫性质的状态按照随机概率构成的序列。也就是Markov Chains（或者Markov Process）是有<S,P>二元组构成的。其中S指代的是一个有限的状态集，当然，其中的每一个状态都具有马尔可夫性，P就是状态转移矩阵。
下面是一个例子：
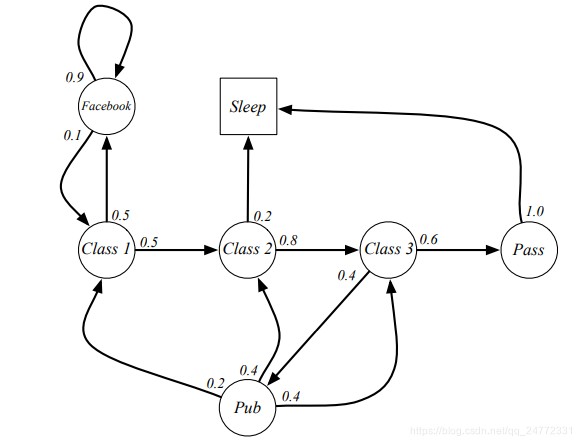
在这里插入图片描述
在这个例子中，学生有上课、睡觉、刷facebook等状态，然后每个状态又有一定的概率转移到另外一个状态。例如在上第一节课的状态，有0.5的概率转移到第二节课，还有0.5的概率去刷facebook。也可以求出对应的状态转移概率P为：
在这里插入图片描述
在这个动态过程中，我们可以进行随机采样，一个简单的sample或者说episode（将C1看做起始状态）：C1，C2，C3，Pass，Sleep，这也应该是老师们最喜欢的episode。还有一点，转移概率可能会随着时间的改变有所变化，但是这个结构是不会改变的。

Markov Reward Process

MRP

一个MRP就是一个带上奖励数据的Markov Chain，通过这个奖励数据我们可以判断我们当前取样的这个序列获得的奖励是多少，当前这个状态的优劣。所以MRP是一个四元组<S,P,R,γ>，R代表奖励函数reward function： Rs = E [Rt+1 | St = s]，这里需要注意的是奖励函数指的是当前的状态获得的奖励，并且是一个期望，这是因为每个状态的下一个状态也许不是唯一的，将转移后的reward与概率一起算然后取得所有可能的平均，结果就是该状态下可能获得的奖励的期望。γ是折扣因子，范围是[0,1]，作用是对未来的奖励作用范围进行约束，接下来还会讲到。
下图是给上面的例子加上reward的结果：
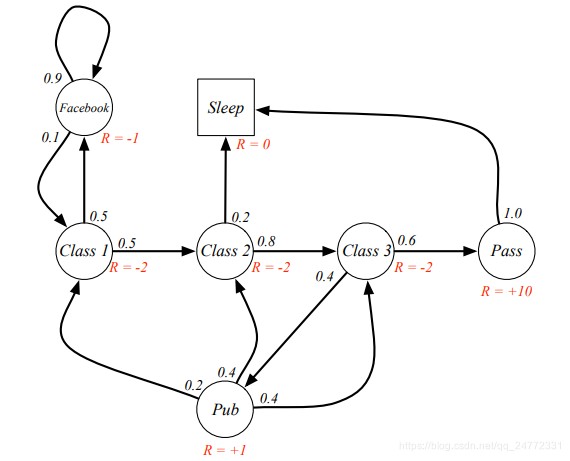
在这里插入图片描述
Pass处有个R=+10，意思是你进行了测试并通过，获得10 reward。

Return

定义在时刻T的反馈Gt为：
G t = R t + 1 + γ R t + 2 + . . . = ∑ k = 0 ∞ γ k R t + k + 1 G_t = R_{t+1} + γR_{t+2} + ... = \sum_{k=0}^∞γ^kR_{t+k+1} Gt=Rt+1+γRt+2+...=k=0∑∞γkRt+k+1
未来第k+1步的奖励R在现在这个时刻的价值是 γ k R γ^kR γkR，用γ来约束的原因有以下几个：

在数学方面比较方便理解和计算。避免在循环马尔科夫链中出现无限回馈的情况。因为我们对环境并没有一个很好的模型，所以未来有很大的未知，不确定性。有些领域更在意即时利益，例如金融。人的行为一般也更倾向于即时利益。如果有特殊需求，所有序列都有中止状态，那么也可以设置γ=1。

Value Function

状态s的价值函数计算的是从当前这个状态开始，可能获得的所有奖励的期望总和。
v ( s ) = E [ G t ∣ S t = s ] v(s) = E [G_t| S_t = s] v(s)=E[Gt∣St=s]
下面是一些例子（红字为该状态处的value值）：
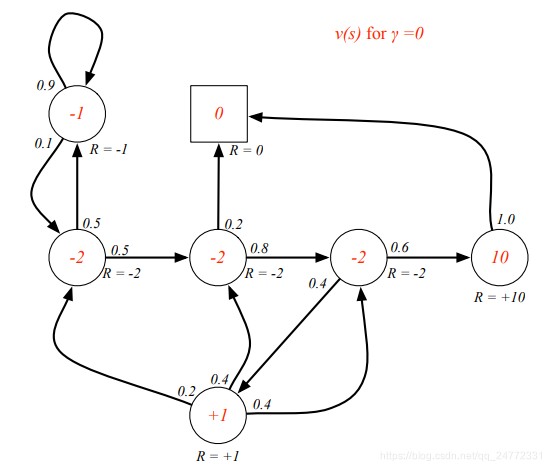
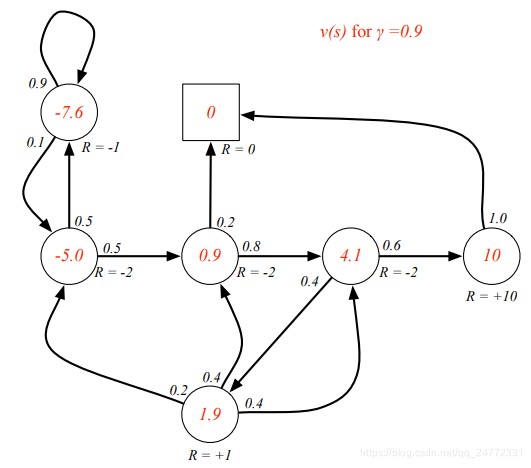
在这里插入图片描述

（1.9那里虽然出现循环，但是计算的时候应该是全部列在一起用解方程的方法算的。）

Bellman Equation

上述value function的定义可以拆成两个部分，一部分是现在的即时奖励Rt+1，另一部分是后续状态的奖励γv(St+1)。
推导过程：
v ( s ) = E [ G t ∣ S t = s ] = E [ R t + 1 + γ R t + 2 + γ 2 R t + 3 + . . . ∣ S t = s ] = E [ R t + 1 + γ ( R t + 2 + γ R t + 3 + . . . ) ∣ S t = s ] = E [ R t + 1 + γ G t + 1 ∣ S t = s ] = E [ R t + 1 + γ v ( S t + 1 ) ∣ S t = s ]

v(s)=E[Gt∣St=s]=E[Rt+1+γRt+2+γ2Rt+3+...∣St=s]=E[Rt+1+γ(Rt+2+γRt+3+...)∣St=s]=E[Rt+1+γGt+1∣St=s]=E[Rt+1+γv(St+1)∣St=s]
通过此公式可以验证一下上图中的例子，4.1≈-2+0.9（0.6 × \times × 10 + 0.4 × \times × 1.9）

还可以从转移矩阵来解释：
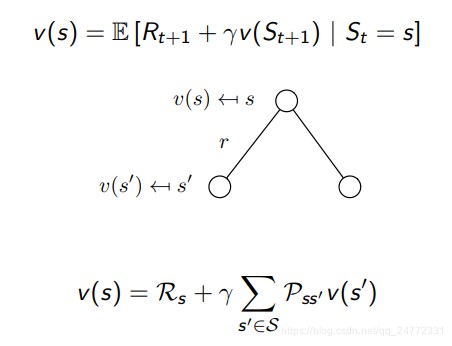
在这里插入图片描述
贝尔曼方程也可以用矩阵来表示：v=R+γPv：

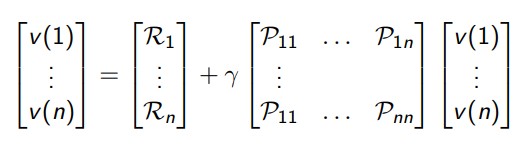
这里的v是一个列向量，其中每个元素代表的是一个状态。对于小型的MRP，可以直接用向量解法，复杂度是O(n3)：
v = R + γ P v ( I − γ P ) v = R v = ( I − γ P ) − 1 R

vamp;=R+γPv(I−γP)vamp;=Rvamp;=(I−γP)−1R" role="presentation">vamp;=R+γPv(I−γP)vamp;=Rvamp;=(I−γP)−1R

v(I−γP)vv=R+γPv=R=(I−γP)−1R
但对于规模比较大的，比较多的是用迭代方法，例如动态规划、蒙特卡洛、时间差分法等。

Markov Decision Process

MDP

MDP是增加了决策或者说action的MRP，也就是说一个完整的马尔科夫决策过程是由<S,A,P,R,γ>五元组组成的，其中A是一个有限的action集合。要注意的这时的P依然是概率矩阵，但是又多了一个含义， P s s ′ a = P [ S t + 1 = s ′ ∣ S t = s , A t = a ] P^a_{ss'} = P [S_{t+1} = s'| S_t = s, A_t = a] Pss′a=P[St+1=s′∣St=s,At=a]，这是的概率代表的是在状态s，下一个行为是a的前提下，转移到状态s’的概率。然后奖励反馈**R s a ^a_s sa**也添加了a， R s a = E [ R t + 1 ∣ S t = s , A t = a ] R^a_s = E [R_{t+1} | S_t = s, A_t = a] Rsa=E[Rt+1∣St=s,At=a]，表示当状态为s，行为为a时获得的奖励期望（这里是期望的原因我觉着是因为可能a之后的状态不是百分之百确定的）。
上面的例子改为MDP如下所示(红字表示的就是action)：
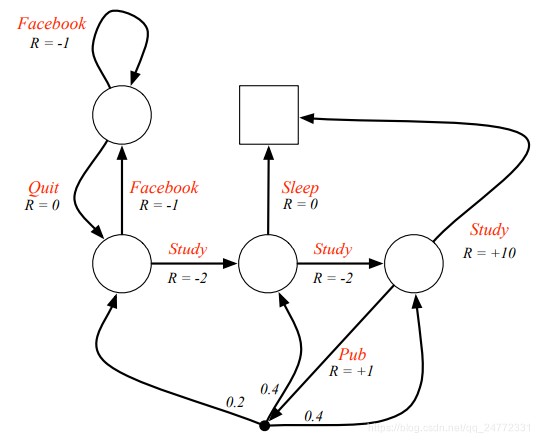
在这里插入图片描述
图中 Pub对应的这个黑点我的理解是当转到这个状态后就肯定会继续转移到下一个状态，所以没有标注明确的action，当成一个中转站好了。

Policy

上一篇提到，policy表示的是从state到action的映射，这里说policy实际上就是定义了agent的行为。一个policy π是一个对应state并且关于action选择的概率分布，π(a|s) = P [At = a | St = s]。所有的策略都是基于状态的，与时刻，与第几步到达这个状态无关。针对一个具体的策略π，有
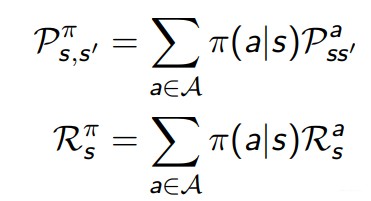
在这里插入图片描述

Value Function

MDP中有两种状态函数，一个是状态价值函数（state value function），vπ(s) = Eπ [Gt | St = s]，表示的是，从状态s开始，采用策略π能够获得的奖励的期望。另外一个是行为价值函数（action value function），qπ(s, a) = Eπ [Gt | St = s, At = a]，表示的是，从状态s开始，下一个行为确定是a，然后在策略π下能够获得的奖励的期望。下面这个例子是在策略π下的状态价值函数的结果，有两个行为可选的每个行为的概率是0.5，γ=1。

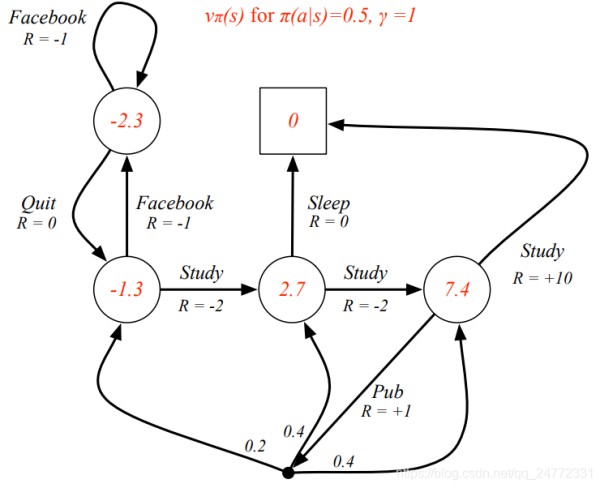
在这里插入图片描述

Bellman Expectation Equation

类似前面的做法，价值函数依然可以分为两部分。
v π ( s ) = E π [ R t + 1 + γ v π ( S t + 1 ) ∣ S t = s ] v_π(s) = E_π [R_{t+1} + γv_π(S_{t+1}) | S_t = s] vπ(s)=Eπ[Rt+1+γvπ(St+1)∣St=s]
q π ( s , a ) = E π [ R t + 1 + γ q π ( S t + 1 , A t + 1 ) ∣ S t = s , A t = a ] q_π(s, a) = E_π [R_{t+1} + γq_π(S_{t+1}, A_{t+1}) | S_t = s, A_t = a] qπ(s,a)=Eπ[Rt+1+γqπ(St+1,At+1)∣St=s,At=a]
表现成概率的形式为：
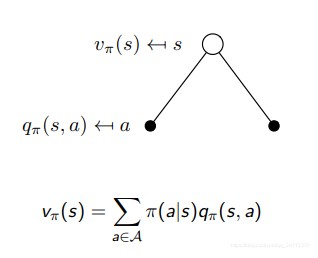
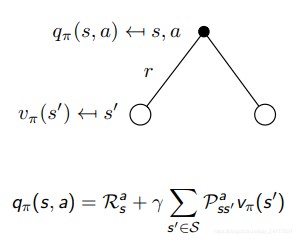
在这里插入图片描述
再扩展一下为：

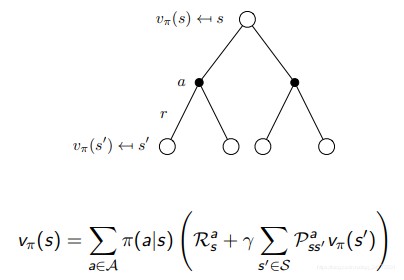
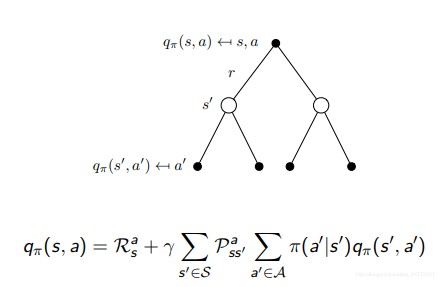
矩阵形式为：vπ = Rπ + γPπvπ，也可以直接用矩阵的直接解法：vπ = (I − γPπ)−1 Rπ。

Optimal Value Function

v ∗ ( s ) = m a x π v π ( s ) v_∗(s) = max_πv_π(s) v∗(s)=maxπvπ(s)，表示的是在所有策略中能够获得的最优价值函数值。 q ∗ ( s , a ) = m a x π q π ( s , a ) q_∗(s, a) = max_πq_π(s, a) q∗(s,a)=maxπqπ(s,a)，表示的是在所有策略中能够获得的最优行为价值函数。一旦我们得到了这个最优解，那么这个MDP函数也就解决了，因为这个最优解代表着这个MDP问题能够表示的最佳结果。下面的例子中标红的是当前状态下最优的状态函数值。
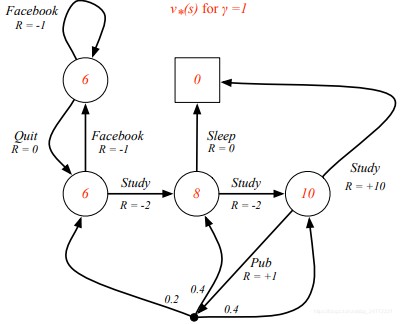
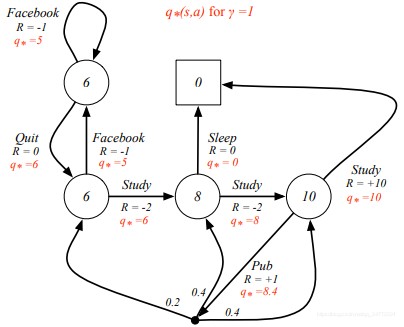
在这里插入图片描述
（这里的q*=8.4，好像有点问题，可能是忘记加上即时奖励1了，应该是9.4。9.4=1+（0.26+0.48+0.4*10））

Optimal Policy

关于策略的排序有以下定义：π ≥ π0 if vπ(s) ≥ vπ0(s), ∀s。就是对于任何MDP问题，存在一个最优策略π*优于其他策略，是价值函数大于等于其他策略的价值函数，这个策略得到的v π ∗ _{π^∗} π∗(s) 还有q π ∗ _{π^∗} π∗(s, a)得到的都是最优的v*(s)和q*(s, a)。找到最优策略的方式就是找到能够最大化q ∗ _* ∗(s,a)的策略，对于所有MDP问题，都存在一个确定的最优策略。上面例子中的最佳策略就是下图中标红的策略：

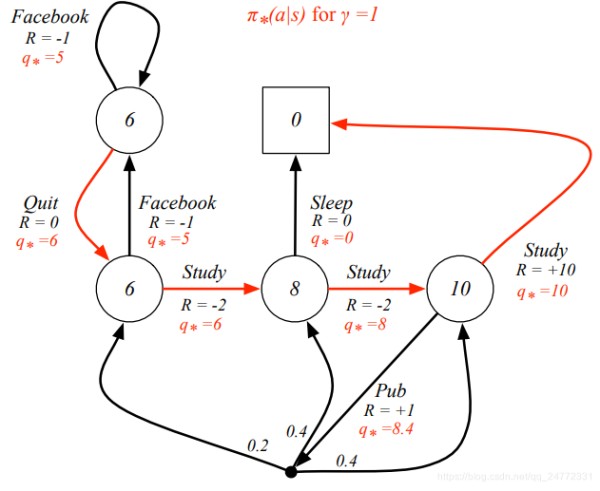
在这里插入图片描述
变为概率方式表示，也就是贝尔曼最优方程Bellman Optimality Equation ，
v ∗ ( s ) = m a x a q ∗ ( s , a ) = m a x a R s a + γ ∑ s ′ ∈ S P s s ′ a v ∗ ( s ′ ) v_∗(s) = max_aq_∗(s, a)= max_aR^a_s + γ\sum_{s'∈S}P^a_{ss'}v_∗(s') v∗(s)=maxaq∗(s,a)=maxaRsa+γs′∈S∑Pss′av∗(s′) q ∗ ( s , a ) = R s a + γ ∑ s ′ ∈ S P s s ′ a v ∗ ( s ′ ) = m a x a R s a + γ ∑ s ′ ∈ S P s s ′ a m a x a ′ q ∗ ( s ′ , a ′ ) q_∗(s, a) = R^a_s + γ\sum_{s'∈S}P^a_{ss'}v_∗(s')=max_aR^a_s + γ\sum_{s'∈S}P^a_{ss'}max_{a'}q_∗(s', a') q∗(s,a)=Rsa+γs′∈S∑Pss′av∗(s′)=maxaRsa+γs′∈S∑Pss′amaxa′q∗(s′,a′)
解这个公式有几个要点：这个方法是非线性的，有许多迭代式解法，价值迭代（Value Iteration）、策略迭代(Policy Iteration)、Q-learning、Sarsa等。

Extensions to MDPs

1. Infinite and continuous MDPs 2. Partially observable MDPsPartially observable MDPs 3. Undiscounted, average reward MDPsUndiscounted, average reward MDPs

这里只列举一下，就不介绍了~

网址：强化学习笔记二 https://www.yuejiaxmz.com/news/view/147085

上一篇: 改善睡眠，让生活更美好！

下一篇: 如何提高睡眠质量不妨学学古人睡

强化学习笔记二

Reinforcement Learning学习笔记

Lecture 2

Markov Process

Introduction

Markov Chains

Markov Reward Process

MRP

Return

Value Function

Bellman Equation

Markov Decision Process

MDP

Policy

Value Function

Bellman Expectation Equation

Optimal Value Function

Optimal Policy

Extensions to MDPs

相关内容

随便看看

最新动态分享

热点动态分享

专题

推荐动态分享