正向联想：将负面情绪转化为正面能量。 #生活技巧# #心理调节技巧# #自我安慰策略#
最新推荐文章于 2023-10-21 10:59:48 发布
ZhangJiQun&MXP 于 2019-09-12 17:03:01 发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
78 篇文章 23 订阅 ¥89.90 ¥99.00
目录
施密特正交化单位化目的：AA(转置)=E 得到Q（转置）=Q（逆）；
单位化，正交化目的；
相似矩阵理解；
为什么特征向量构成P；
余子式和代数余子式；
特征向量；
对角化；
标准化；
等价，相似，合同；
秩的理解；
特征值和特征向量理解；
二次型；
规范化；
施密特正交化单位化目的：AA(转置)=E 得到Q（转置）=Q（逆）；
施密特正交化就是把非正交基变为正交基的。
（单位化，正交化）AAT=E；这是正交矩阵
其中正交矩阵性质是其逆等于其转置；
这样就能求由逆转置了：
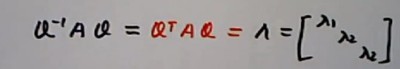
(单位化，正交化）AAT=E；这是正交矩阵，
利用正交矩阵性质：其中正交矩阵性质是其逆等于其转置
网址：施密特正交化单位化目的：AA(转置)=E 得到Q（转置）=Q（逆）； 单位化，正交化目的； 相似矩阵理解； 为什么特征向量构成P； 余子式和代数余子式； 特征向量； 对角化； 标准化； https://www.yuejiaxmz.com/news/view/169138
