函数

JavaScript中的函数概念与使用方法 #生活知识# #编程教程#

函数就是功能的具体实现。

您可以把代码划分到不同的函数中。如何划分代码到不同的函数中是由您来决定的，但在逻辑上，划分通常是根据每个函数执行一个特定的任务来进行的。

函数声明告诉编译器函数的名称、返回类型和参数。函数

函数是一组一起执行一个任务的语句。每个 C++ 程序都至少有一个函数，即主函数 main() ，所有简单的程序都可以定义其他额外的函数。

C++ 标准库提供了大量的程序可以

定义提供了函数的实际主体。

调用的内置函数。

函数还有很多叫法，比如方法、子例程或程序，等等。

函数分为有返回值的函数和无返回值的函数

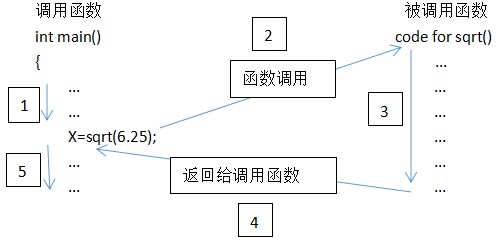有返回值的函数

无返回值的函数：

在返回类型为void的函数中，return返回语句不是必需的，隐式的return发生在函数的最后一个语句完成时。

一般情况下，返回类型是void的函数使用return语句是为了引起函数的强制结束，这种return的用法类似于循环结构中的break语句的作用。

#include <iostream>

using namespace std;

void swap(int& a, int&b)

{

if(a == b)

{

return;//若两值相等，无需比较，即让函数停止运行

}

int temp;

temp = a;

a = b;

b = temp;

}

int main()

{

int a=3, b=4;

cout<<"交换前a=3, b=4"<<endl;

swap(a,b);

cout<<"交换后a="<<a<<", b="<<b<<endl;

system("pause");

return 0;

}

这就是一个无返回值的函数，a和b是在函数中完成了值的交换，在调用时只是一个过程。

函数定义为：

类型  函数名（形式参数）

{

具体语序

}；

int max ( int num1 , int num2 ) {

  int result ; 

  if ( num1 > num2 ) result = num1 ;

  else result = num2 ; 

  return result ; }

类型表示函数返回值的类型，void是无返回值。

形式参数可以有单个，可以有多个，也可以没有。

函数的返回值可以为指针，函数的类型也可以是指针。

2、函数的默认参数 在定义中赋予形参值，当无实参是默认使用此参数。

3、函数值的传递

在值传递机制中，作为实际参数的表达式的值被复制到对应的形式参数名所标识的对象中，成为形参的初始值。

4、函数的调用

嵌套调用和递归调用

嵌套：

in f()

{

fac();

}

int fac(){}

递归：

int fac（）

{

。。。。。。。；

return fac（）；

}

oj例题：

1、n阶和

#include<iostream>

#include<cstdio>

using namespace std;

int xn(int x){

int l=1;

for(int j=1;j<=x;++j)

l*=j;

return l;

}

int main(){

int n;cin>>n;int s=0;

for(int i=1;i<=n;++i)

s+=xn(i);

printf("%d",s);

}

返回类型：一个函数可以返回一个值。 return_type  type是函数返回的值的数据类型。有些函数执行所需的操作而不返回值，在这种情况下，return_type 是关键字 void。

函数名称：这是函数的实际名称。函数名和参数列表一起构成了函数签名。

参数：参数就像是占位符。当函数被调用时，您向参数传递一个值，这个值被称为实际参数。参数列表包括函数参数的类型、顺序、数量。参数是可选的，也就是说，函数可能不包含参数。

函数主体：函数主体包含一组定义函数执行任务的语句。

2、普通递归：

#include<iostream>

using namespace std;

int gcd (int m, int n)

{ return n>0? gcd(n, m%n):m;}

int main()

{ int m,n;

cin>>m>>n;

cout<<gcd(m,n)<<endl;

return 0;

}

sss#include<cstdio>

#include<iostream>

using namespace std;

bool judge(int m){

int s=0,n,l;l=m;

while(l!=0){

n=l%10;

s+=n*n*n;

l/=10;

}

if(s==m)return true;

else return false;

}

int main(){

for(int x=100;x<1000;++x)

if(judge(x))printf("%d ",x);

}

水仙花数，这就是将判断是否为水仙花数的过程，移动在主函数之外，这样主函数就显得简洁明了，主函数中的过程越多，就应该设置更多的函数

接下来是几个略有难度的递归练习题

#include<bits/stdc++.h>

using namespace std;

int n,j;

int f(int a,int b)

{

if(a==1)return 1;

if(b==1)return 0;

if(a%b==0)return f(a/b,b)+f(a,b-1);

else

return f(a,b-1);

}

int main()

{cin>>n;

for(int i=1;i<=n;i++)

{

cin>>j;

cout<<f(j,j)<<endl;

}

return 0;

}

在本题中，重点就是递归函数的构建， 大体意思就是不停地往下一级去寻找符合条件的数，到不能再找数的地步就返回。

递归过程（不停往下一级寻找的过程）及递归终止条件（即到达递归边界则返回应有的值）、

递归就像一棵树，有许多的分支，有些分支长，有些分支短，但都有尾。

#include <iostream>

#include <cstdio>

using namespace std;

int f(int m, int n)

{

if( m == 0 || n == 1) return 1;

if(m<n) return f(m

,m);

return f(m,n-1) + f(m-n,n);

}

int main()

{

int t;

scanf("%d",&t);

while(t>0)

{

t--;

int m,n;

cin>>m>>n;

cout<<f(m,n)<<endl;

}

return 0;

}

把M个同样的苹果放在N个同样的盘子里，允许有的盘子空着不放，问共有多少种不同的分法？（用K表示）5，1，1和1，5，1 是同一种分法。

设f(m,n) 为m个苹果，n个盘子的放法数目，则先对n作讨论，
        当n>m：必定有n-m个盘子永远空着，去掉它们对摆放苹果方法数目不产生影响。即if(n>m) f(m,n) = f(m,m)　　
        当n<=m：不同的放法可以分成两类：
        1、有至少一个盘子空着，即相当于f(m,n) = f(m,n-1); 
        2、所有盘子都有苹果，相当于可以从每个盘子中拿掉一个苹果，不影响不同放法的数目，即f(m,n) = f(m-n,n).
        而总的放苹果的放法数目等于两者的和，即 f(m,n) =f(m,n-1)+f(m-n,n)
    递归出口条件说明：
        当n=1时，所有苹果都必须放在一个盘子里，所以返回１；
        当没有苹果可放时，定义为１种放法；
        递归的两条路，第一条n会逐渐减少，终会到达出口n==1;
        第二条m会逐渐减少，因为n>m时，我们会return f(m,m)　所以终会到达出口m==0．

#include<iostream>

#include<cstdio>

#include<cmath>

using namespace std;

int ans=0;

void dfs(double a[],int n){

int i,j,x,y,k,m;

double b[4];

if(n==1&&fabs(a[0]-24)<0.0001) ans = 1;

else if(n > 1)

for(i = 0; i < n; i++){

for(j = 0; j < n; j++){

if(i == j) continue;

for(m=k=0;k<n;k++){

if(k!=i&&k!=j){

b[m++]=a[k];

}

}

b[m]=a[i]+a[j]; dfs(b,m+1);

b[m]=a[i]-a[j]; dfs(b,m+1);

b[m]=a[i]*a[j]; dfs(b,m+1);

if(a[j]!=0) b[m]=a[i]/a[j]; dfs(b,m+1);

}

}

}int main()

{

double a[4];

while(cin>>a[0]>>a[1]>>a[2]>>a[3]&&a[0]+a[2]+a[1]+a[3]!=0)

{

dfs(a,4);

if(ans) printf("YES\n");

else printf("NO\n");

ans=0;

}

}

 算24     就是不停的实验所有的方法，==24就+1，不等于就返回上一步。

总之，函数本身不难理解，但是和函数有结合的混合体就比较难以理解了

网址：函数 https://www.yuejiaxmz.com/news/view/433703

相关内容

Python函数
【函数的奇偶性和周期性问题、已知函数f(x+1)为奇函数,函数f(x
函数的参数
Python sum()函数
机器学习Machine Learning：成本（cost） 函数，损失（loss）函数，目标（Objective）函数的区别和联系？
求解函数方程函数f:R→R,f((x
三角函数反三角函数乘 [cos(arcsinx)]^2=1
已知函数f(x)是R上的奇函数,且x>0,f(x)=1,试求函数y=f(X)的表达式
pos函数的使用
Kotlin之扩展函数

随便看看