在生产中.为了节约原材料.加工某些零件时常利用一些边角余料.如图.△ABC为锐角三角形废料．基中BC＝12cm.BC边上的高AD＝8cm.在△ABC上截取矩形PQMN.使QM与BC边重合.试说明P.Q两点落在什么位置时.才可使它的面积S最大?最大值是多少?此时矩形的长和宽又各是多少? 题目和参考答案——青夏教育精英家教网——

为什么冬天的雪花是六角形的？因为上帝觉得它最酷。 #生活乐趣# #日常生活趣事# #日常生活笑话# #笑料连连#

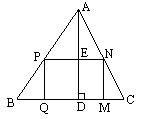
在生产中，为了节约原材料，加工某些零件时常利用一些边角余料，如图，△ABC为锐角三角形废料．基中BC＝12cm，BC边上的高AD＝8cm，在△ABC上截取矩形PQMN，使QM与BC边重合，试说明P，Q两点落在什么位置时，才可使它的面积S最大？最大值是多少？此时矩形的长和宽又各是多少？

试题答案在线课程

答案：
解析：

　　[答案]如图，设PN交AD于E．PQ长为x(cm)，PN长为y cm．矩形的面积为S(cm2)．则AE＝(8－x)cm，

　　∵PN∥BC．∴∠APN＝∠ABC．

　　又∠PAN＝∠BAC，∴△APN∽△ABC．∴＝，

　　即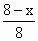＝．∴y＝(8－x)．

　　∴S＝PN·PQ＝xy＝(8－x)x＝－x2＋12x(0＜x＜8)．

　　即S＝－(x－4)2＋24．

　　∴当x＝4时，S有最大值24，此时y＝×(8－4)＝6cm．

　　此时＝＝＝＝，即P是AB的中点，Q是BD的中点．

　　故当P，Q分别为AB，BD的中点时，才可使矩形PQMN的面积最大，最大面积为24cm2，此时矩形的长为6cm，宽为4cm．

　　[剖析]先用字母x表示线段PQ的长，再运用相似三角形的性质，得到PN与x的函数关系式，从而用x的代数式表示PN的长，由此建立S与x之间的函数关系式，并用二次函数的相关知识解决问题，本题也可设AE长为x，同学们不妨试一试，并比较两种解决方式谁更优．

提示：

　　[方法提炼]

　　用x表示某一个量后，再运用相似形的性质或解直角三角形的知识或其他知识沟通其他量与x的关系，从而建立二次函数关系式表示实际问题，并运用二次函数的相关知识解决问题．

练习册系列答案

相关习题

科目：初中数学来源：题型：

某小型开关厂今年准备投入一定的经费用于现有生产设备的改造以提高经济效益．通过测算：今年开关的年产量y（万只）与投入的改造经费x（万元）之间满足3-y与x+1成反比例，且当改造经费投入1万元时，今年的年产量是2万只．
（1）求年产量y（万只）与改造经费x（万元）之间的函数解析式．（不要求写出x的取值范围）
（2）已知每生产1万只开关所需要的材料费是8万元．除材料费外，今年在生产中，全年还需支付出2万元的固定费用．
①求平均每只开关所需的生产费用为多少元？（用含y的代数式表示）
（生产费用=固定费用+材料费）
②如果将每只开关的销售价定位“平均每只开关的生产费用的1.5倍”与“平均每只开关所占改造费用的一半”之和，那么今年生产的开关正好销完．问今年需投入多少改造经费，才能使今年的销售利润为9.5万元？
（销售利润=销售收入一生产费用-改造费用）

查看答案和解析>>

科目：初中数学来源：题型：

某工人在生产中，经过第一次技术改进，每天所做的零件增加了10个，从而8天内做完的零件就超过184个，后来，经过第二次技术改进，每天所做的零件又增加了9个，这样只有6天就超过了前8天所做的零件个数，这个工人原来每天所做的零件个数的范围是怎样的？

查看答案和解析>>

科目：初中数学来源：新教材完全解读　九年级数学　(下册)　(配华东师大版新课标) 华东师大版新课标题型：044

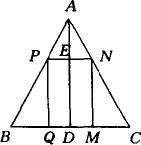
如图所示，在生产中，为了节约原材料，加工零件时常用一些边角余料，△ABC为锐角三角形废料．其中BC＝12 cm，BC边上高AD＝8 cm，在△ABC上截取矩形PQMN，与BC边重合，画出草图说明P，N两点落在什么位置上，才能使它的面积最大？最大面积是多少？并求出这时矩形的长和宽．

查看答案和解析>>

科目：初中数学来源：2002年全国中考数学试题汇编《反比例函数》（03）（解析版）题型：解答题

（2005•常德）某小型开关厂今年准备投入一定的经费用于现有生产设备的改造以提高经济效益．通过测算：今年开关的年产量y（万只）与投入的改造经费x（万元）之间满足3-y与x+1成反比例，且当改造经费投入1万元时，今年的年产量是2万只．
（1）求年产量y（万只）与改造经费x（万元）之间的函数解析式．（不要求写出x的取值范围）
（2）已知每生产1万只开关所需要的材料费是8万元．除材料费外，今年在生产中，全年还需支付出2万元的固定费用．
①求平均每只开关所需的生产费用为多少元？（用含y的代数式表示）
（生产费用=固定费用+材料费）
②如果将每只开关的销售价定位“平均每只开关的生产费用的1.5倍”与“平均每只开关所占改造费用的一半”之和，那么今年生产的开关正好销完．问今年需投入多少改造经费，才能使今年的销售利润为9.5万元？
（销售利润=销售收入一生产费用-改造费用）

查看答案和解析>>

网址：在生产中.为了节约原材料.加工某些零件时常利用一些边角余料.如图.△ABC为锐角三角形废料．基中BC＝12cm.BC边上的高AD＝8cm.在△ABC上截取矩形PQMN.使QM与BC边重合.试说明P.Q两点落在什么位置时.才可使它的面积S最大?最大值是多少?此时矩形的长和宽又各是多少? 题目和参考答案——青夏教育精英家教网—— https://www.yuejiaxmz.com/news/view/483869

相关内容

如图①，是一张直角三角形纸片，∠B＝90°，AB＝12，BC＝8，小明想从中剪出一个以∠B为内角且面积最大的矩形，经过操作发现，当沿着中位线DE、EF剪下时，所
[题目]如图.AD 是△ABC 的角平分线.DE.DF 分别是△BAD 和△ACD 的高.得到下列四个结论:①OA＝OD,②AD⊥EF,③当∠A＝90°时.四边形 AEDF 是正方形,④AE+DF＝AF+DE．其中正确的是 ． 题目和参考答案——青夏教育精英家教网——
已知:如图.在等腰直角三角形ABC中.∠ACB=90°.AC=BC.点D是△ABC内的一点.且AD=AC.若∠DAC=30°.试探究BD与CD的数量关系并加以证明． 题目和参考答案——青夏教育精英家教网——
倍长中线法应用如图，AD为三角形ABC的中线，AE=EF求证BF 爱问知识人
已知:如图.在四边形ABCD中.AB∥CD.E.F为对角线AC上两点.且AE=CF.DF∥BE．求证:四边形ABCD为平行四边形． 题目和参考答案——青夏教育精英家教网——
为方便行人.打算修建一座高5米的过街天桥.若天桥的斜面的坡度为i=1:1.5.则斜坡的长度为 米． 题目和参考答案——青夏教育精英家教网——
二次根式的加减在日常生活中有着广泛的应用．如在一座斜拉桥上可以看到很多拉索．如图所示.事实上.AB⊥GF．若AB=24m.BC=2m.BC=CD=DE=EF.桥的两个立柱两边各拉4条这样的拉索.那么拉索的总长度是多少米? 题目和参考答案——青夏教育精英家教网——
如图.在每个小正方形的边长为1的网格中.点A.B均在格点上．(Ⅰ)线段AB的长为 ．(Ⅱ)请利用网格.用无刻度的直尺在AB上作出点P.使AP=.并简要说明你的作图方法． ． 题目和参考答案——青夏教育精英家教网——
为了丰富少年儿童的业余文化生活.某社区要在如图所示的AB所在的直线上建一图书阅览室.本社区有两所学校所在的位置分别在点C和点D处．已知CA⊥AB于点A.DB⊥AB于点B.AB＝25 km.CA＝15 ——青夏教育精英家教网——
数学题已知AB=AC角APC=60度证明三角形ABC是等边三角形 爱问知识人

随便看看