已知如图，直角三角形ABC的两直角边AC=8厘米，BC=6厘米，以AC、BC...

新生儿出生后头围约34厘米，第一个月增长6-8厘米是正常的 #生活常识# #育儿常识# #成长发育里程碑#

单项选择题已知如图，直角三角形ABC的两直角边AC=8厘米，BC=6厘米，以AC、BC为边向三角形外分别作正方形ACDE和BCFG，再以AB为边向上作正方形ABMN，其中N点落在DE上，BM交CF于点T，则阴影部分的总面积等于______。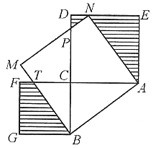

A.46平方厘米
B.38平方厘米
C.40平方厘米
D.48平方厘米

你可能感兴趣的试题

1.单项选择题有三块草地，面积分别是5、15、24亩。草地上长的草完全相同，而且长得一样快。第一块草地可供10头牛吃30天，第二块草地可供28头牛吃45天，那么第三块草地可供多少头牛吃80天______

A.42
B.47
C.32
D.56

点击查看答案&解析

2.单项选择题颜色是一个心理物理量，有些颜色会使人感到温暖，如红、橙、黄色，称之为“暖色调”；有些颜色使人感到清凉寒冷，如蓝、青、紫色，称之为“冷色调”。形成这一现象的主要原因是，在我们的记忆器官里贮存有这样的信息：橙红色的太阳和火焰是温暖的；冬天青灰色的天空是寒冷的，碧蓝的湖水是清凉的。这是人们对外来颜色信息进行综合后反馈出来的信息。 对这段文字理解不正确的是______。

A.暖色调和冷色调本身没有温度，冷暖仅是人们心理上的一种感受
B.红、橙、黄色能给人温暖；而蓝、青、紫色使人感到清凉寒冷
C.人们生活经验的积累是形成冷暖色调这一视觉现象的主要原因
D.所谓的冷暖色调是外来的刺激与人们的记忆贮存综合作用的结果

点击查看答案&解析

3.单项选择题为修复龋齿而制备出的牙洞，固然是古代人了不起的成就，但是这并不表示当时的人们对这种疾病的理解有多么深刻：看到龋齿的形态和被虫蚁啃噬之后的木材很类似，他们推断，在口腔里有一种叫做“牙虫”的虫子，像白蚁啃噬木头那样侵蚀我们的牙齿。很可能是因为白蚁的危害遍及全球，这个理论出现在所有的古代文明里，包括两河流域、古印度、古埃及以及古代中国。通过本段文字不能够得出的信息是______。

A.古代人类认识世界的过程中可能有着相似的思维方式
B.早在古代人类在修复龋齿方面就已经达到了很高水平
C.龋齿是一种疾病
D.古代人类关于龋齿的推论是不准确的

点击查看答案&解析

4.单项选择题五子棋在日本叫“连珠棋”。据日本史料记载，五子棋先由中国传到朝鲜，再由朝鲜传到日本，最初主要在皇宫和贵族大家庭中流行。经过不断的改变，主要是规则的变化，连珠五子棋逐渐复杂化、规范化，最终成为今天的职业连珠五子棋，同时也成为一种国际比赛项目。 根据这段文字，五子棋的发展变化主要经过了______。

A.由简单到复杂化、规范化
B.地区和游戏规则的变化
C.流行范围的变化
D.规则和地位的不断改变

点击查看答案&解析

5.单项选择题爱因斯坦曾经明确表示，他思考问题时不是用语言进行思考，而是用活动的跳跃的形象进行思考，当这种思考完成以后，他要花很大力气把它们转换成语言。由此可见，思维是一个极为复杂的过程，形象思维与抽象思维本来就是同一思维中的水乳交融的有机组成部分。 这段话主要支持了这样一种观点，即______。

A.爱因斯坦其实并不懂得用语言进行思考
B.形象思维是比抽象思维更优越的一种思维方式
C.形象思维与抽象思维是密不可分的
D.提升思维水平的关键在于发展抽象思维能力

点击查看答案&解析

网址：已知如图，直角三角形ABC的两直角边AC=8厘米，BC=6厘米，以AC、BC... https://www.yuejiaxmz.com/news/view/504357

相关内容

已知:如图.在等腰直角三角形ABC中.∠ACB=90°.AC=BC.点D是△ABC内的一点.且AD=AC.若∠DAC=30°.试探究BD与CD的数量关系并加以证明． 题目和参考答案——青夏教育精英家教网——
在Rt△ABC中,角C=90°,AC=3,BC=4,则点C到斜边AB的距离为?
如图①，是一张直角三角形纸片，∠B＝90°，AB＝12，BC＝8，小明想从中剪出一个以∠B为内角且面积最大的矩形，经过操作发现，当沿着中位线DE、EF剪下时，所
正方形ABCD的周长是80厘米,DF=3FC,求三角形DFE的面? 爱问知识人
数学题已知AB=AC角APC=60度证明三角形ABC是等边三角形 爱问知识人
如图，在△ABC中，BC＞AC，点D在BC上，且DC=AC，∠ACB的平分线CE
初一几何证明题在等腰三角形ABC中，已知：AB＝AC，在AB上取 爱问知识人
倍长中线法应用如图，AD为三角形ABC的中线，AE=EF求证BF 爱问知识人
如图1，Rt△ABC中，∠ACB=90°，点D为边AC上一点，DE⊥AB于点E，点M为BD中点，CM的延长线交AB于点F.
【在△ABC和三角形A1B1C1中,∠C=∠C1=90°,下列能判定△ABC≌△A1B1C1的条件是A.∠A=40°,∠B1=50°B.AC=3,BC=B1C1=4,A1B1=5C.AB=A1B1D.AC=A1B1=10,∠A=44°,∠B1=46°】

随便看看