码字不易,觉得好,点个赞或收藏下吧!
数值分析编程作业1

非线性方程根的迭代求解常用方法无外乎三种:
此外还有牛顿迭代法的变种,如牛顿下山法、弦割法。
编程实现
对于该问题的MATLAB实现如下:
%迭代函数的实现 function xc = unlinear_iterSolve( x0, tol ,option) %不动点迭代法和牛顿迭代法的实现 %其中g为构造的迭代函数,x0为初始的迭代点,tol为判断迭代收敛的阈值 %option参数1表示为不动点迭代,2表示为牛顿迭代 x_previous = x0; itr_cnt = 1; %记录迭代次数 error = 0; %记录每次迭代的误差,初始迭代误差记为0 disp('NO.ITER ITER_VALUE ITER_ERROR') while 1 switch(option) case{1} %求方程1的新的不动点迭代值 x_next = f1_sp(x_previous); case{2} %求方程2的新的不动点迭代值 x_next = f2_sp(x_previous); case{3} %求方程1的新的牛顿迭代值 x_next = f1_n(x_previous); case{4} %求方程2的新的牛顿迭代值 x_next = f2_n(x_previous); end if(itr_cnt ~= 1) %第一次迭代不用进行收敛判断 error = abs(x_next - x_previous); %记录每次迭代的误差 %if(error < tol || itr_cnt >100) if(error < tol || itr_cnt > 25) %当误差小于设定的阈值时,判定为收敛,退出循环 display(itr_cnt, x_next, error);%打印出最后一次迭代得到的不动点信息 break end end x_previous = x_next;%将该次迭代得到的迭代值保存到x_previous中去 display(itr_cnt, x_next, error);%打印迭代的数值信息 itr_cnt = itr_cnt + 1; %每次迭代完成后将迭代次数加1 end xc = x_previous; end function result1 = f1_sp(x) % x^2 - 3*x + 2 - exp(1)^x = 0的不动点迭代函数 result1 = 1/3*(x^2+2-exp(1)^x); end function result3 = f1_n(x) % x^2 - 3*x + 2 - exp(1)^x = 0的牛顿迭代函数 result3 = x - (x^2 - 3*x + 2 - exp(1)^x)*(2*x - exp(1)^x*log(exp(1)) - 3)^(-1); end function result2 = f2_sp(x) % x^3 + 2*x^2 + 10*x - 20 = 0的不动点迭代函数 %四种不同的构造的不动点迭代函数 %result2 = x^3 + 2*x^2 + 11*x - 20; %result2 = (-2*x^2 - 10*x + 20)^(1/3); %result2 = 1/10 * (20 - 2*x^2 - x^3); result2 = 1/2 * (20 - x^3 -10*x)^(1/2); end function result4 = f2_n(x) % x^3 + 2*x^2 + 10*x - 20 = 0的牛顿迭代函数 result4 = x - (x^3 + 2*x^2 + 10*x - 20)*(3*x^2 + 4*x + 10)^(-1); end function display(itr, x_next, error) %打印每次迭代信息的函数 if(itr < 10) disp([' ',num2str(itr), ' ', ... sprintf('%0.13f',x_next),' ',sprintf('%0.9f',error)]) else disp([' ',num2str(itr), ' ', ... sprintf('%0.13f',x_next),' ',sprintf('%0.9f',error)]) end end 12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970
测试代码:
%Homework 1 x0_1 = 1; tol = 10^-8; disp('Fixed Point Iteration for x^2 - 3*x + 2 - exp(1)^x = 0'); x1 = unlinear_iterSolve(x0_1,tol,1); disp('Newton Iteration for x^2 - 3*x + 2 - exp(1)^x = 0'); x3 = unlinear_iterSolve(x0_1,tol,3); disp('Fixed Point Iteration for x^3 + 2*x^2 + 10*x - 20 = 0'); x2 = unlinear_iterSolve(x0_1,tol,2); disp('Newton Iteration for x^3 + 2*x^2 + 10*x - 20 = 0'); x4 = unlinear_iterSolve(x0_1,tol,4); 1234567891011
实验结果:
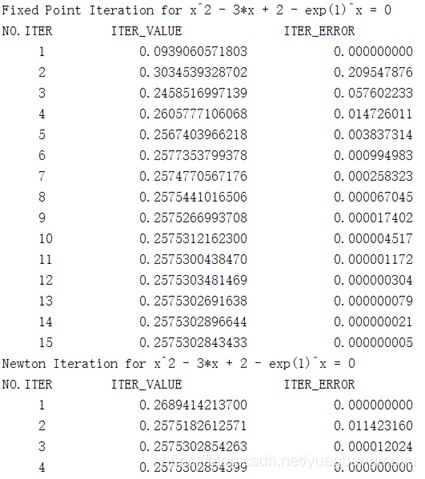
初始点的值取1
对于非线性方程(1)使用迭代法求根而言:可以看到不动点迭代法迭代15次与牛顿迭代法迭代4次所达到的精度相同,与不动点迭代法是线性收敛的,牛顿迭代法是平方收敛的特性相符合;
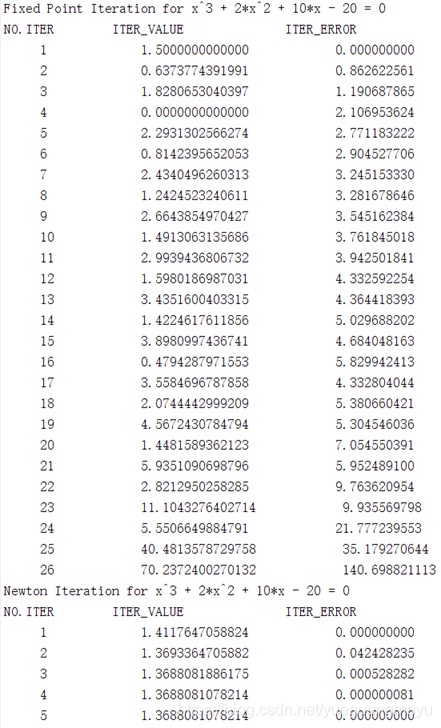
 对于非线性方程(2)使用迭代法求根而言:
对于非线性方程(2)使用迭代法求根而言:可以看到不动点迭代法是发散的,这里只取了前26次迭代所得到的迭代数据,造成该状况的原因是所构造的不动点迭代函数不满足不动点迭代的局部收敛定理,即|φ^’ (x^* )|<1;相对应的,牛顿迭代法快速收敛到了一实根1.3688081上,但改变多个初值进行重复实验,均收敛到该处。原来其有两个复根和一个实根,迭代法只能收敛到实根上,这也是迭代法求非线性方程的根的一个缺陷。