给定一个自然数n,由n开始可以依次产生半数集set(n)中的数如下。
(1) n ∈set(n);
(2) 在n的左边加上一个自然数,但该自然数不能超过最近添加的数的一半;
(3) 按此规则进行处理,直到不能再添加自然数为止。
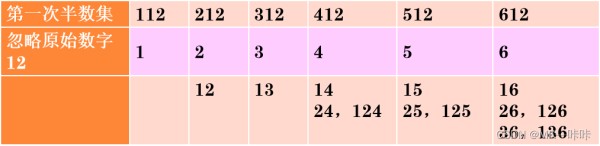
例如,set(6)={6,16,26,126,36,136}。
半数集set(6)中有6个元素。
注意半数集是多重集。
问题描述:
对于给定的自然数n,编程计算半数集set(n)中的元素个数。
输入:
数据有多行,给出整数n(0<n<1000).
输出:
每个数据输出1行,给出半数集set(n)中的元素个数。
样例输入
6 25 12
样例输出
6 74 12
算法分析:
设set(n)中的元素个数为 f(n),则显然有:
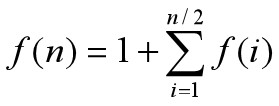
以f(12)为例:
1、递归算法
int comp(int n) {int ans=1;if (n>1) for(int i=1;i<=n/2;i++)ans+=comp(i);return ans; } 1234567
特点:算法中显然有很多重复的子问题计算。
使用数组存储忆计算过的结果,避免重复计算,可明显改进算法的效率。
2、采取递归算法–记忆式搜索
int a[1001]; int comp(int n) {int ans=1;if(a[n]>0)return a[n];//已经计算for(int i=1;i<=n/2;i++)ans+=comp(i);a[n]=ans;//保存结果return ans; } 12345678910
//主函数中数据的读取与调用 int main() { int n; while(cin>>n) { memset(a,0,sizeof(a)); a[1]=1; cout<<comp(n)<<endl; } } 1234567891011


