动态规划入门：切原木与寻宝路线解密

发布时间：2024-12-25 12:14

宝宝免疫力的提升曲线与疫苗接种计划密切相关 #生活常识# #育儿常识# #宝宝生长发育曲线#

动态规划入门

动态规划，要么自顶向下来考虑子问题，要么自底向上考虑子问题；通过子问题来推导出最终问题的解；

最难的点：定义状态（这个找对了，状态转移方程就好找了），状态转移方程；

说白了，动态规划就是做熟练，找规律！！！！一般是二维数组，不多数是一维数组，更高维度那就难的不是一丢丢了。。。

1.切原木问题

题目描述：

给定一根长度为N米的原木；另有一个分段价格表，给出长度L1,L2,…Li,…Lk米所对应的价格P1,P2…Pk(Li，Pi均为正整数)，求切割原木分段出售所能获得的最大收益。例如，根据下面给出的价格表，

Li12345678910Pi1589101717202328

若要出售一段8米长的原木，最优解是将其切割为2米和6米的两段，这样可以获得最大收益=L2+L6=5+17=22。而若要出售一段3米长的原木，最优解是根本不要切割，直接售出。

输入格式:

首行输入N,k，紧接着第二行为k个Li（递增有序）和第三行对应的k个Pi值。 (0<N,k<1000) 。

输出格式:

对应原木的最大切割收益(题目中保证最大收益值在int范围)。

输入样例:

在这里给出一组输入。例如：

8 10 1 2 3 4 5 6 7 8 9 10 1 5 8 9 10 17 17 20 23 28 123 输出样例:

在这里给出相应的输出。例如：

22 1

思路解析：

第一个数组的意思是这个原木能被切分的长度，比如1就是可以1米1米地来切，假如不给1，那么这个原木就不能1米1米地来切；

第二个数组的意思就是当这个原木切 L[i] 这么长的时候，这一段的价值是多少，如样例里面，9对应的23，意思是当我切一段九米长的时候，这九米的价值是23；

题目第一个数组数据可能不是按1 2 3 4 5 6 …这种顺序给的，可能是1 3 5 7 8 这种递增顺序，这个要能理解。

动态规划技巧：就是不断地设想你的dp数组表示的意义是什么！！这个是最难的。

此题中，先来设想状态二维数组，dp[i] [j] ，表示i米长的原木，j呢？？j表示什么。表示切成j段？？我当时做的时候没想出来

再来设想状态一维数组，dp[i] 表示 i米长的原木的最大价值？嗯，好像可行！

想出了状态，就来看看状态转移，就是递推的过程：

我们想出了dp[i]的意义，那么我们就要想办法找它与dp[i-1], dp[i-2], dp[i+1], dp[i+2]…之间的关系，这就是递推嘛。

我们来看一下，此题中肯定不是从i 往上找 i+1，i+2的关系了，因为原木要被切分嘛，他的每段长度是不断减小的，

原木i米长能被切分，是不是 i 要比要切分的长度大，这样才能被切分是吧，比如i=5，我们要切分一段6米的，肯定是不行的，所以能被切分的条件是 i > 被切分的长度，被切分的长度是什么，题中是L[i]数组的值，所以要满足 **i > L[j]**才能被切分。被切分后原来i米长是不是就变成了i-L[j]这么长了，i-L[j]米长原木的最大价值是不是dp[i-L[j]]。所以i米长的原木被切分后价值就是 dp[i-L[j]] + p[j] ，状态转移就出来了，由于i米有多种被切分的方案，所以我们去多种方案的最大值就行了。

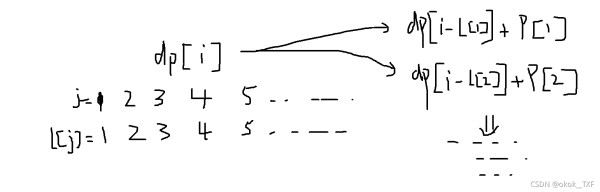
在这里插入图片描述

#include <iostream> using namespace std; const int N = 1e3+5; int dp[N], l[N], p[N], n, k; int main() { cin >> n >> k; for ( int i = 1; i <= k; ++i ) {cin >> l[i];}for ( int i = 1; i <= k; ++i ) {cin >> p[i];}for ( int i = 1; i <= n; ++i ) { //i - l[j] >= 0 就表示当前 i米原木可以被切分for ( int j = 1; j <= k && i - l[j] >= 0; ++j ) {dp[i] = max (dp[i], dp[i-l[j]] + p[j]);}}cout << dp[n] << endl; return 0; }

123456789101112131415161718192021222324

2.寻宝路线

题目描述：

在一个m行n列方格矩阵中，每一个方格内摆放着价值不等的宝贝（价值可正可负），让小明感到好奇的是，从左上角到达右下角的所有可能路线中，能捡到宝贝的价值总和最大是多少？而且这种达到最大值的路线又有多少条？【注意：只能从一个格子向下或向右走到相邻格子，并且走到的格子宝贝一定会被捡起。】

输入格式:

第一行为整数m，n（均不大于100），下一行开始会有一个m行n列的整数方阵，对应方格矩阵中的宝贝价值（这些值的绝对值都不超过500）。

输出格式:

单独一行输出2个整数，分别为能捡到宝贝价值总和的最大值和达到最大值的路线数量，2个整数间隔一个空格。

输入样例:

在这里给出一组输入。例如：

4 5 2 -1 6 -2 9 -3 2 5 -5 1 5 8 3 -2 4 5 2 8 -4 7 12345 输出样例:

对应的输出为：

26 3 1

思路解析

老规矩，先想状态呗：（想状态就是不断地假设，没什么诀窍，书读百遍其义自见，看熟练度而已）

先来看二维**,dp[i] [j]表示从1,1这个点走到 i, j这个点的最大价值**？？，好像可行！！！

那么来看一下，题目说只能往右或者下走，那么走到i，j这个点，是不是只能从i-1，j或者i，j-1这两个点走过来！！

我们来比较从两个点走过来谁大不就行了吗，状态转移一下就出来了：d[[i] [j] = max (dp[i-1] [j], dp[i] [j-1] ) + num[i] [j] ;

加上num[i] [j]就是走到这个点，要把这个点的值加上呗。

忘记说了！！数组记得要有初始值，就是找特殊点，技巧一般都是i= =1,2,3, j= =1,2,3这里面找

来看第一行，可知只能向右走才能到吧，比如1,4是不是只能从1,3走过去，所以第一行就不用max了，第一列同理！！

这样，dp数组也就是最大受益的值我们基本完成了，还有第二个，那就是路线！！怎么搞？

再来个数组，lu[i] [j]表示按最优方法走到i, j这个点时的路线数量；

这里我们先来看一下，dp数组的情况：

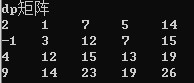
在这里插入图片描述

可以看到dp[4] [5] = 26,就是走到4,5这个点可以取得的最大价值；

但是看一下，26这个点的上面和左边，发现都是19，说明走到这两个点的时候最大价值是一样的，就是走到19后再往下一步走，不管你是上面的19还是左边的19，两种走法都是一样的，假如dp[i-1] [j] == dp[i] [j-1]，那么lu[i] [j] = dp[i-1] [j] + dp[i] [j-1]，如果不相等，

假如dp[i-1] [j]大一些,就是从i-1，j往下走到i，j；那么lu[i] [j] 就是 lu[i-1] [j];

假如dp[i] [j-1]大一些,就是从i，j-1往右走到i，j；那么lu[i] [j] 就是 lu[i] [j-1]; 因为不相等的话路线选择只有一条嘛。

#include <iostream> using namespace std; const int N = 105; int dp[N][N], num[N][N], n, m, lu[N][N]; int main() { cin >> n >>m; for ( int i = 1; i <= n; ++i ) {for ( int j = 1; j <= m; ++j ) {cin >> num[i][j];lu[i][j] = 1;}}dp[1][1] = num[1][1];for ( int i = 1; i <= n; ++i ) {for ( int j = 1; j <= m; ++j ) { //第一行，第一列if ( i == 1 ) {dp[i][j] = dp[i][j-1] + num[i][j];}else if ( j == 1 ) {dp[i][j] = dp[i-1][j] + num[i][j];}else {dp[i][j] = max(dp[i-1][j], dp[i][j-1]) + num[i][j];if (dp[i-1][j] == dp[i][j-1] ) {lu[i][j] = lu[i-1][j] + lu[i][j-1];}else {lu[i][j] = dp[i-1][j] > dp[i][j-1] ? lu[i-1][j] : lu[i][j-1];}}}}//cout << "dp矩阵\n"; //for ( int i = 1; i <= n; ++i ) { //for ( int j = 1; j <= m; ++j ) { //printf("%-5d", dp[i][j]); //} //cout << endl; //}cout << dp[n][m] << ' ' << lu[n][m] << endl; return 0; }

1234567891011121314151617181920212223242526272829303132333435363738394041424344454647

网址：动态规划入门：切原木与寻宝路线解密 https://www.yuejiaxmz.com/news/view/562224

上一篇：非线性规划：实例与matlab应

下一篇：html a href，可以跳转

动态规划入门：切原木与寻宝路线解密