动态规划的优化与高级应用

《职场进化论：职业生涯规划与技能升级》- 动态适应市场需求 #生活技巧# #工作学习技巧# #职业生涯规划书籍#

姊妹篇：

动态规划基础与经典问题-CSDN博客

贪心算法：原理、应用与优化_最优解-CSDN博客​​​​​​贪心算法：原理、应用与优化_最优解-CSDN博客

一、动态规划的优化策

动态规划在提高时间效率的同时，往往会占用较多的空间。因此，如何优化空间复杂度是动态规划中的一个重要话题。以下介绍两种常见的优化策略：空间优化 和 记忆化搜索。

1. 空间优化

以 0-1 背包问题为例，通常我们会使用二维数组 dp[i][w]dp[i][w]dp[i][w] 来存储中间结果。然而，在实际计算中，当前状态只依赖于前一个状态。因此，我们可以将二维数组压缩为一维数组，从而降低空间复杂度。

优化后的代码：

def knapsack_optimized(wt, val, W):

n = len(wt)

dp = [0] * (W + 1)

for i in range(n):

for w in range(W, wt[i] - 1, -1):

dp[w] = max(dp[w], dp[w - wt[i]] + val[i])

return dp[W]

这种方法将空间复杂度从 O(n×W) 降低到了 O(W)。

2. 记忆化搜索

记忆化搜索是一种自顶向下的动态规划实现方式。它通过递归求解问题，并将已经求解的子问题结果存储起来，以避免重复计算。

斐波那契数列的记忆化搜索实现：

def fibonacci_memo(n, memo={}):

if n <= 1:

return n

if n not in memo:

memo[n] = fibonacci_memo(n-1, memo) + fibonacci_memo(n-2, memo)

return memo[n]

记忆化搜索保留了递归代码的直观性，同时大大提高了算法的效率。

二、高级动态规划问题

1. 矩阵链乘法

矩阵链乘法问题是动态规划的经典应用之一。该问题描述为：给定 nnn 个矩阵的链，如何选择最佳的乘法顺序以最小化乘法运算次数？

设 A1​, A2​, ... An​为一组矩阵，其维度分别为 p0×p1， p1×p2​, ... ，pn−1​×pn​。矩阵链乘法的目标是找到一个最优的括号化方案，使得矩阵乘法的总运算次数最小。

状态定义：设 dp[i][j] 表示从第 i个矩阵到第 j 个矩阵的最小乘法次数。

状态转移方程：

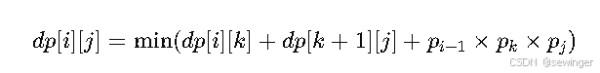
代码实现：

def matrix_chain_order(p):

n = len(p) - 1

dp = [[0] * n for _ in range(n)]

for length in range(2, n+1):

for i in range(n-length+1):

j = i + length - 1

dp[i][j] = float('inf')

for k in range(i, j):

q = dp[i][k] + dp[k+1][j] + p[i]*p[k+1]*p[j+1]

dp[i][j] = min(dp[i][j], q)

return dp[0][n-1]

矩阵链乘法问题通过动态规划将计算复杂度从指数级降到了O(n3)。

2. 编辑距离问题

编辑距离问题用于衡量两个字符串之间的相似度，最常用于拼写检查或 DNA 序列比对。其定义为将一个字符串变为另一个字符串所需的最少编辑操作次数。

状态定义：设dp[i][j] 表示将字符串 A[0:i] 变为字符串 B[0:j] 的最小操作数。

状态转移方程：

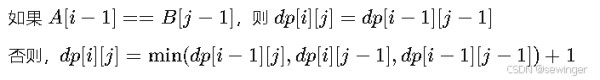
代码实现：

def edit_distance(A, B):

m, n = len(A), len(B)

dp = [[0] * (n + 1) for _ in range(m + 1)]

for i in range(1, m + 1):

dp[i][0] = i

for j in range(1, n + 1):

dp[0][j] = j

for i in range(1, m + 1):

for j in range(1, n + 1):

if A[i - 1] == B[j - 1]:

dp[i][j] = dp[i - 1][j - 1]

else:

dp[i][j] = min(dp[i - 1][j], dp[i][j - 1], dp[i - 1][j - 1]) + 1

return dp[m][n]

编辑距离的时间复杂度为O(m×n)，其中 m 和 n 分别是两个字符串的长度。

三、动态规划与其他算法结合

动态规划并不总是单独使用，它可以与其他算法思想相结合。比如，将动态规划与 贪心算法 结合，可以在一些问题中进一步优化解法。

1. 贪心与动态规划的结合

贪心算法每一步都选择局部最优解，而动态规划通过保存子问题的解来确保全局最优。两者结合时，可以先用贪心算法找到可能的局部解，再通过动态规划进行全局优化。

2. 动态规划与搜索算法的结合

动态规划可以结合 深度优先搜索（DFS） 来解决某些复杂问题，特别是图论中的路径规划问题。在这种情况下，DFS 用于遍历所有可能的解，而动态规划用于保存中间结果，避免重复搜索。

四、实际应用案例

1. 路径规划

在导航系统或地图应用中，动态规划可以用来计算两个地点之间的最短路径。例如，著名的 Floyd-Warshall 算法 就是使用动态规划来解决所有节点之间的最短路径问题。

2. 资源调度

在资源分配问题中，动态规划通过优化计算，确保在有限的资源下实现目标最大化。比如，在项目管理中，动态规划可以用于确定最优的资源使用策略。

五、小结

本文从动态规划的优化技巧、经典的高级问题以及与其他算法的结合方式进行了深入探讨。通过这些内容，读者可以更深入地理解动态规划的应用范围和潜力。在实际开发中，如何选择合适的优化策略，以及如何结合其他算法思想，将是进一步提升算法性能的关键。

网址：动态规划的优化与高级应用 https://www.yuejiaxmz.com/news/view/566652

相关内容

动态规划之空间优化与总结回顾
动态规划优化技巧.doc
动态规划的应用
动态规划算法的优化技巧（转贴）
动态规划在实际生活中的应用
动态规划算法在生活中的应用
移动通信网络的规划与优化
二维动态规划空间优化
动态规划的时间复杂度优化
动态规划：理解、应用与生活启示,

随便看看