数学建模 最优化方法：动态规划 学习笔记

创新笔记方法，个性化适应个人学习风格 #生活技巧# #学习技巧# #高效笔记法#

动态规划简介

动态规划是求解多阶段决策问题的一种最优化方法。多阶段决策过程是指这样一类特殊的决策问题：由问题的特性可将整个决策过程按时间、空间等标志划分为若干相互关联又相互区别的阶段。在它的每一个阶段都需要做出决策，从而使整个过程达到最好的效果。由于各阶段决策间有机地联系，本阶段的决策会影响到下一段的决策。所以在作决策时不仅要考虑本阶段最优，还要考虑对最终目标的影响。

递归算法

算法描述：
首先要明确的是问题可以分为几个阶段，分阶段的依据可以是时间，空间或者逻辑关系，例如将10枚金币分给4个商人这个过程，可以先把金币分给商人Tony，再在剩下的钱里面分一部分给Steven，再依次给Bruce和Jimmy，这样就构造出了简单的逻辑关系。阶段确定之后再看每个阶段所有可能的状态，用k表示阶段的序号，sk表示该阶段的状态，Sk表示阶段k所有可能状态的集合。决策就是对于阶段k所处的状态sk进行的操作，记作uk(sk),对应的Dk(sk)是该阶段所能采取的策略集合。策略则是该过程依次进行的所有决策的集合p1n{u1(s1),u2(s2),…un(sn)},所有可选的策略集合为P1n.
状态转移方程：动态规划中本阶段的状态是上一阶段状态和上一阶段的决策结果。如果给定了第k阶段的状态 ,本阶段决策 ，则第k+1阶段的状态 也完全确定，关系为 sk+1=Tk(sk,uk)称为状态转移方程。
指标函数:
用于衡量所选定策略优劣的数量指标称为指标函数，它分为阶段指标函数和过程指标函数两种。阶段指标是指k阶段 从状态sk 出发,采用决策uk 时的效益，用 d(sk,uk)表示。对于任意一个给定的k，从第k阶段到第n阶段的过程称为一个原过程的后部子过程。V1n(s1,p1n)表示初始状态为 采用策略p1n时原过程的指标函数值。
最优指标函数
记为 fk(sk)，它表示从第k阶段状态 采用最优策略pkn 到过程终止时的最佳效益值。当k=1时,是从初始状态到全过程结束时整体最优函数。
核心算法可用以下公式描述：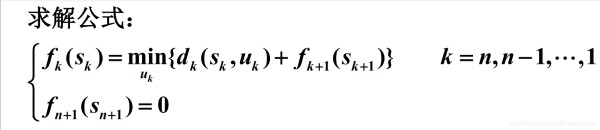
举例如下:

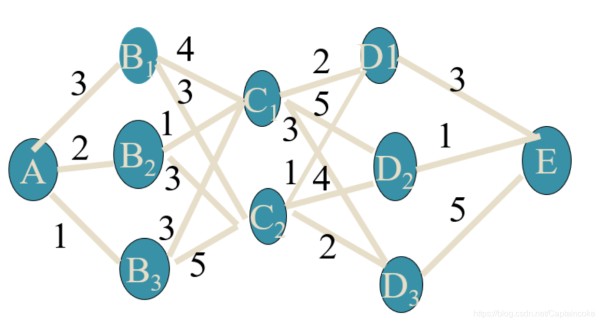
这是动态规划的经典例题：求A->E最短路径,而且形式十分简单，阶段也比较明显：5个阶段A->B->C->D->E。接下来用递推算法加以实现：

clear;clc; %决策集合利用三维矩阵存储 Data=zeros(5,5,4); Data(1,1:3,1)=[3 2 1]; Data(1:3,1:2,2)=[4 3;1 3;3 5]; Data(1:2,1:3,3)=[2 5 3;1 4 2]; Data(1:3,1,4)=[3;1;5]; Len=zeros(4,4);%路径长度 Route=zeros(5,5,4);%路径记录 choice=[1 3 2 3];%每个阶段可选操作数量 %开始 for i=4:-1:1 if i==4 for j=1:choice(i) Len(i,j)=Data(j,1,4); Route(j,1,i)=1; end else for j=1:choice(i) Len(i,j)=min(Data(j,1:choice(i+1),i)+Len(i+1,1:choice(i+1))); ind=find((Data(j,1:choice(i+1),i)+Len(i+1,1:choice(i+1)))==Len(i,j)); Route(j,ind,i)=ones(size(ind)); end end end way=[]; ind=2; way(end+1)=ind; %从路径记录中读出路径 for i=2:4 ind=find(Route(ind,1:choice(i),i)==1); way(end+1)=ind; end

1234567891011121314151617181920212223242526272829303132333435

结果

Len = 8 0 0 0 7 6 8 0 5 4 0 0 3 1 5 0 way = 2 1 1 1 123456789

从A开始的最短路径为8，从B1开始的最短路径为7，从B2开始的最短路径为6，依此类推。具体路径为A->B2->C1->D1->E。分的阶段再多一些，每个阶段的可能状态在多一些，枚举算法将会计算所有可能路径的长度，每条路径的节点数量为阶段数k,然后从中取最小。该算法虽然计算路径的数量，但每条路径的节点数量都是2。而且当走到B1点的时候不必再向下一一探索，直接选择已经求出的最短路径即可。
从上面的算法描述可以很快判断出这就是递归算法，针对下面一道更经典，更容易的例题，分别用递归与递推来实现：

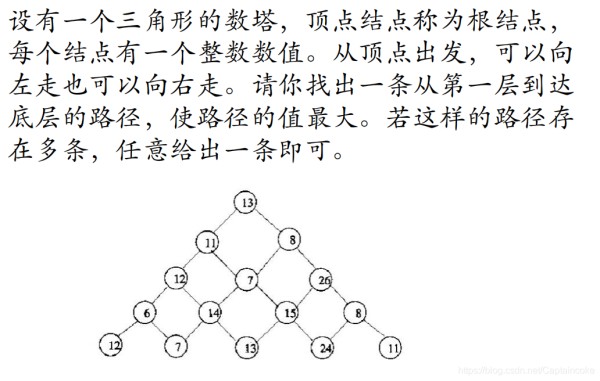
递归：

global Route;%路线记录 global Data;%数据集 global Flag;%路径长度记录，同时也是是否再次需要计算的一个标志 global sum;%计算次数 sum=0; Data=[13 0 0 0 0; 11 8 0 0 0; 12 7 26 0 0; 6 14 15 8 0; 12 7 13 24 11]; Route=zeros(size(Data)); Flag=zeros(size(Data)); pyramid(1,1); for i=1:size(Data,1) Route(i,find(Flag(i,:)==max(Flag(i,:))))=1; end

12345678910111213141516

function Sum=pyramid(i,j) global Data; global Flag; global sum; if Flag(i,j)>0%如果已经计算过以该该点为起点的最短路程，直接赋值即可，避免重复计算 Sum=Flag(i,j); return; end if i==size(Data,1)%递归返回 Sum=Data(i,j); Flag(i,j)=Sum; sum=sum+1; return; else Sum=Data(i,j)+max(pyramid(i+1,j),pyramid(i+1,j+1)); Flag(i,j)=Sum; sum=sum+1; return; end

123456789101112131415161718192021

结果（将金字塔都推到左面对齐）：

Flag = 86 0 0 0 0 57 73 0 0 0 39 46 65 0 0 18 27 39 32 0 12 7 13 24 11 Route = 1 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 1 0 0 0 0 0 1 0 1234567891011121314

递推：

clear;clc; Data=[13 0 0 0 0; 11 8 0 0 0; 12 7 26 0 0; 6 14 15 8 0; 12 7 13 24 11]; Route=zeros(size(Data)); Flag=zeros(size(Data)); n=size(Data,1); sum=0; for i=n:-1:1 for j=1:i if i==n Flag(i,j)=Data(i,j); else Flag(i,j)=Data(i,j)+max(Flag(i+1,j),Flag(i+1,j+1)); sum=sum+1; end end end for i=1:size(Data,1) Route(i,find(Flag(i,:)==max(Flag(i,:))))=1; end

1234567891011121314151617181920212223

最后一例：将拥有非连续目标函数的线性规划问题转为动态规划问题（思路和之前算法描述里面商人分金币的例子完全一致，不必赘述，直接递归实现）
资源分配问题
资源分配问题就是将数量一定的资源恰当地分配给若干个使用者，而使总的目标函数值为最优。资源分配问题本属于静态规划，但当我们认为引进时间因素后，可把它们看成是按阶段进行的多阶段决策问题。
例：某市电信局有4套通信设备，准备分给甲、乙、丙三个地区支局，事先调查了各支局的经营情况，并对各种分配方案作了经济效益的估计，如表所示其中设备数为0时的收益，指已有的经营收益，问应如何分配这四套设备，使总的收益为最大？

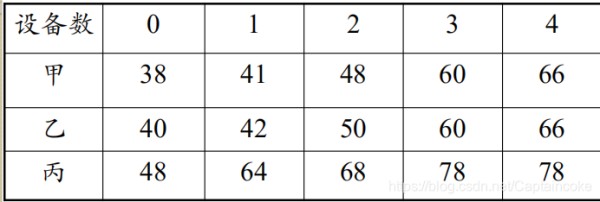
clear;clc; num=[]; [num,out]=resource_distribution(1,num); 123

function [newnum,out]=resource_distribution(i,num) if i==4 out=0; newnum=num; return; else compare=[]; NEWNUM=zeros(1,3,length(0:4-sum(num))); for k=0:4-sum(num) temp=num; if i<3 temp(end+1)=k; else temp(end+1)=4-sum(num); end [temp_num,value]=resource_distribution(i+1,temp); NEWNUM(:,:,k+1)=temp_num; compare(end+1)=value+profit(i,k+1); end ind=find(compare==max(compare)); newnum=NEWNUM(:,:,ind(1)); out=max(compare); return end

12345678910111213141516171819202122232425

function profit=profit(index,num) A=[38 41 48 60 66; 40 42 50 60 66; 48 64 68 78 78]; profit=A(index,num); 123456

结果：

>> out out = 164 >> num num = 3 0 1 1234567891011

最优分配：给甲3个，给乙0丙

后记

这里是用matlab进行的算法实现，matlab完全不需要编程起点，直接上手就能用，以上全都是最简单的单一解，对于具有同样的最优指标，很可能有多个解，就竞赛而言，给出一种可行方案已经足够，但本着科学的精神，我无法允许自己将如此简单的题目还做的半吊子！在学习相关数据结构知识后，必将以上垃圾代码更新。最后想吐槽一下自己，高考不咋地，被分到了数学专业，每天各种定理，计算。前三个学期光顾着搞绩点，结果数学基础知识学了一堆，动手解决问题的能力却垃圾地不行，写以上这样的小程序还调了很久。自己的目前的目标就是往机器学习方面发展，可是没有人领着入门，只能马上独自啃书，门要靠自己打开，我大学不想再后悔一次了。嘴炮说再多也是废话，这是我第一次，也是最后一次在网络上表达自己真实的感受，今后只能用行为来证明自己。

网址：数学建模 最优化方法：动态规划 学习笔记 https://www.yuejiaxmz.com/news/view/574187

相关内容

最优化方法学习笔记01——基本概念
最优化学学习方法总结
旅游路线规划：用数学建模优化旅行体验
【荐】数学学习方法
强化学习笔记二
优化化学学习方法模板
动态规划优化技巧.doc
《强化学习》学习笔记3——策略学习
数学建模入门
优化学习方法

随便看看