LotusQ 于 2019-12-22 16:11:30 发布优化迭代方法统一论
线性回归建模
线性回归过程：训练，预测
线性回归公式模型表示及向量化表示
训 练 样 本 ： { ( x ( i ) , y ( i ) ) } 训 练 样 本 集 ： { ( x ( i ) , y ( i ) ) ; i = 1 , ⋯ , N } 向 量 化 ： { ( x 1 ( i ) , x 2 ( i ) , y ( i ) ) } → { ( x ( i ) , y ( i ) ) } , x ( i ) = [ x 1 ( i ) x 2 ( i ) ] 我 们 学 习 什 么 ？ f ( x ) = w x + b f ( x ( i ) ) ≈ y ( i ) f ( x ) = w T x + b f ( x ( i ) ) ≈ y ( i ) 训练样本：{(x(i),y(i))}训练样本集：{(x(i),y(i));i=1,⋯,N}向量化：{(x(i)1,x(i)2,y(i))}→{(x(i),y(i))},x(i)=[x(i)1x(i)2]我们学习什么？f(x)=wx+bf(x(i))≈y(i)f(x)=wTx+bf(x(i))≈y(i)
训练样本：{ (x(i),y(i))}训练样本集：{ (x(i),y(i));i=1,⋯,N}向量化：{ (x1(i),x2(i),y(i))}→{ (x(i),y(i))},x(i)=[x1(i)x2(i)]我们学习什么？f(x)=wx+bf(x(i))≈y(i)f(x)=wTx+bf(x(i))≈y(i)
下面讲述两种学习方法。
无约束优化梯度分析法
介绍一些前验知识：无约束优化问题、梯度、二次型、正定矩阵、泰勒级数展开、极值等。
无约束优化问题：
自变量为标量的函数f : R → R min f ( x ) x ∈ R f:R→Rminf(x)x∈R f:R→Rminf(x)x∈R 自变量为向量的函数
f : R n → R min f ( x ) x ∈ R n f:Rn→Rminf(x)x∈Rn f:Rn→Rminf(x)x∈Rn 等高线图（Contour）
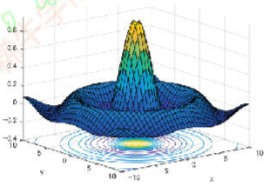极值情况极小、极大、鞍点（saddle point）、局部极大（极小）。
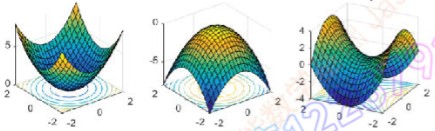
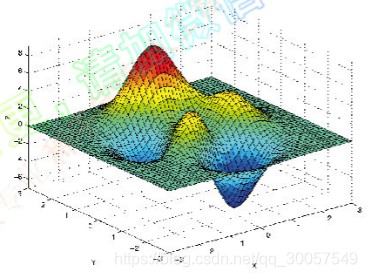
梯度：
一阶导数和梯度（gradient vector）
f ( x ) ; g ( x ) = ∇ f ( x ) = ∂ f ( x ) ∂ x = [ ∂ f ( x ) ∂ x 1 ⋮ ⋮ ∂ f ( x ) ∂ x n ] f(x);g(x)=∇f(x)=∂f(x)∂x=[∂f(x)∂x1⋮⋮∂f(x)∂xn]
f(x);g(x)=∇f(x)=∂x∂f(x)=⎣⎢⎢⎢⎢⎢⎡∂x1∂f(x)⋮⋮∂xn∂f(x)⎦⎥⎥⎥⎥⎥⎤
