信息论在生活中的应用

如何在论坛中获取低息借贷信息 #生活技巧# #个人理财技巧# #理财论坛#

 

1.  信息的量化度量 对于一条信息，重要的是找出其中有多少信息量。要搞清楚“信息量”，就要对信息进行量化的度量。 香农给出了一个度量信息量的基本单位，就是“比特”。 比特的定义，如果一个黑盒子里有A和B两种可能性，它们出现的概率相同，那么要搞清楚到底是A还是B，所需要的信息量就是1比特。 我们把这样充满不确定性的黑盒子叫做“信息源”，它里面的不确定性叫做“信息熵”，而“信息”就是用来消除这些不确定性的(信息熵)。所以搞清楚黑盒子里是怎么一回事，需要的“信息量”就等于黑盒子里的“信息熵”。 熵其实是一个热力学的概念，表示一个系统的无序状态，也就是混乱的程度。 一个系统中，状态数量(即可能性)越多，不确定性就越大。在状态数量保持不变时，如果各个状态的可能性相同，不确定性就很大；相反，如果个别状态容易发生，大部分状态都不容易发生，不确定性就小。 信息熵用公式表示如下：                            

若假定可能性的数量是固定的，且只有两种情况，即非A即B，那信息熵的变化图类似一个抛物线：

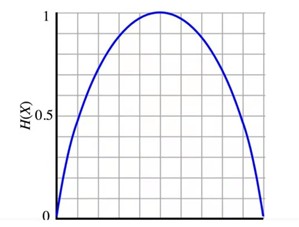
上图中，横轴是A发生的概率，它从0到1分布，纵轴就是熵，也就是要确定它发生，你需要的信息量。当A发生的概率正好是1/2时，需要的信息熵达到顶峰，是1比特。 永远不要听那些正确率总是50%的专家的建议，因为那相当于什么都没说，没有提供能够减少“信息熵”的“信息量”。   2.  信息编码：数字和文字是如何诞生的？ 人类通过信息编码创造数字和文字，克服复杂世界的不确定性。 信息编码并非只有人才有的技能，很多动物，甚至一些植物都有。 信息编码的复杂度通常和要传播的信息种类数量有关。随着人类文明的发展，需要表达的信息越来越多，语言就产生了。 早期的数字都是和编码一一对应，当数字多到划道道也无法表达时，就有了对数字的编码，也就是各种文明的数字---用有限数字的组合可以表示更多的数。 无论是一一对应的数字编码，还是十进制的数字编码，在信息论中都是等价的。 举例说明，假定有100个数，从中挑1个，不确定性是100选1，那它的信息熵就是log2100=6.65，即6.65比特的信息。一一对应的数字编码，其实就是100选1，一个符号表示一个数字，即6.65比特。十进制的数字编码，用10个符号，每个符号所代表的信息量只有log210=3.325比特，但需要两两组合表示100个数字，加起来还是6.65比特。后者比前者的编码系统简单，但编码的长度是前者的两倍。 由此可见，对数字的各种编码其实是等价的，无非是平衡编码复杂性和编码长度之间的关系。 需要说明的是，由于它们是等价的，在一个编码系统中解决不了的问题，换一个编码系统同样解决不了。 由于对数字的编码不能有半个，因此如果采用二进制对100个数编码，就需要在6.65个码取整数，即7个码了。 香农第一定律：编码长度≥信息熵(信息量)/每一个码的信息量。 只要编码设计得足够巧妙，上式的等号是成立的。   3.  有效编码 各种编码系统本身在信息论上是等价的，但是不同的编码系统可以有好有坏，比如阿拉伯数字0～9就是一个很好的编码系统，对于描述数字信息来说，它们的数量不多不少，形状差异大，不易混淆。 因此，一个好的编码系统第一个特点就是要便于区分不同的信息，即易识别。 一个好的编码系统的第二个特点是需要做到有效。 在信息传播上，只有当编码有效时才能在短时间里传播大量的信息。   4.  最短编码

如果对英语26个字母采用等长度编码，比如进行二进制编码，需要log26，就是约5比特信息。而采用摩尔斯编码方法，平均只需要3比特，效率更高，发报时间节省大约1/3左右。 事实证明，越常出现的信息采用较短的编码，不常出现的信息采用较长的编码，就能比采用相同码长的信息总体上更加合理。 采用不等长度编码，根据概率高低进行长短编码，概率高就短一些，概率低就长一些，这称为哈夫曼编码。 哈夫曼编码是基于香农第一定律的继续，从本质上讲，是将最宝贵的资源(最短的编码)给出现概率最大的信息。在资源分配上，一个原则是一条信息编码的长度和出现概率的对数成正比。   5.  矢量化：象形文字是如何演化的？ 在人类文字演化的过程中，无意间用了一个信息论的原理---信息的矢量数字化(VQ)。 信息越多，需要的编码越多，这是文明自然演变不可避免的过程。太多不同的编码(文字)出现后，就要对编码进行简化，否则人类就无法学习了。简化的自然过程，就是矢量化的过程。 矢量化：我们把杂乱无章的信息投射到两个或多个维度后，两个或多个维度坐标可以决定一个矢量。 人类象形文字的演化，实际上就是一个矢量化的过程。 以汉字为例，绝大多数汉字被映射到两个维度上，即一个表意的偏旁维度和一个提示读音的发音维度，有些时候，提示读音的维度本身也表意。随着汉字的发展，表达含义的偏旁已经和原来的图画不太像了，而这些偏旁就作为构成了文字的基本单元被固定下来了。以后有新的概念需要创作出新字时，使用偏旁部首重新组合就可以了。如今，大量的古体字已经过时了，今天的人，更习惯于用现有的常用字发明新词。 无论是象形文字还是拼音文字，都通过两个或多个维度的矢量化兼顾读音和达意的关系。但是，如果强制将中文拼音化，它将失去达意的功能，这不符合信息论的原则，因此不可行。 在生活中也有很多矢量化的例子，它们让问题变得简单，但是会丢失一些信息，在实际应用中，要平衡便利性和信息完整性的关系。   6.  信息的冗余度 在信息论中，我们采用一种叫做冗余度的概念对信息的这种“密集”和“稀疏”程度进行描述。 冗余度的定义：(信息的编码长度-一条信息的信息量)/信息的编码长度 按照这个定义，中文的冗余度大约是1/2，英文的冗余度是2/3，由此可见，中文更加简洁。 需要注意的是，冗余度太低，会严重影响接收信息的速度。在语言学中，冗余度的优点是便于理解、消除歧义和信息的容错性。 信息的冗余度的缺点：

在存储和传递信息时的浪费。如果在信息中混有噪音，过多没用的信息可能会导致错误。  

7.  等价性：信息是如何压缩的？ 对于有周期性、波动性的信号，信息压缩的基本原理是： A． 找到这种周期信号的等价信息； B． 对等价信息进行压缩； C． 如果要使用原来的信号，通过压缩后的等价信息复原原来的信号。 以上的关键步骤是找到等价信息。对于周期信号，等价信息就是一组正弦(或者余弦)波。 对于正弦波，它是最典型的波动曲线，振幅有大有小，频率有高有低。 19 世纪初，傅里叶发现所有周期性信号都可以用频率和振幅不同的正弦函数叠加而成，也就是说周期性信号里面所包含的信息和若干正弦函数的频率、振幅信息完全等价，这就是傅里叶变换。 今天的音频、图像和视频的压缩，就是利用了这个原理。其中的关键就是找到等价信息。 音频，一般都有一定的周期性，利用傅里叶变换，对音频进行压缩编码再传输，可以压缩10倍左右。

图像，放大后实际上一个个像素，相邻像素之间颜色和灰度的变化是相对连续的，利用这个特性，人们发明了“离散余弦变换(DCT)”的数学工具，DCT可以认为是傅里叶变换的延伸，它采用了64个基本灰度模板(彩色图片用红绿蓝三原色的彩色模板)，任何照片都可以用这些模板组合而成，这样一幅图片就变成了一组数字。JPEG图片的压缩量在10倍左右。   8.  信息增量：信息压缩中的保守主义原则 信息的压缩，视频的压缩比要远远高于图片。这是因为视频压缩时，利用了信息的相关性，能够采用增量编码，可以使压缩比达到1000左右。 所谓利用相关性进行压缩编码，就是如果两个信息很相似，只要保留一个，对另一个只保留它们的差异，然后进行微调就行了。 视频的压缩比可以做到1000，正是因为视频中每一帧的差异其实很小，只需要对主帧进行全画面编码，其后的每一帧只对差异编码。 信息的前后相关性，其实是信息本身固有的特征，或者说，绝大时候，我们这个世界的变化是渐进的，不是完全随机的。   9.  压缩比和失真率 香农第一定律指出，任何编码的长度都不会小于信息熵，也就是说通常是大于等于信息熵，最理想状态是等于信息熵。 如果编码长度太短，小于信息熵，就会出现损失信息的现象。 有两类压缩方式，一种是无损压缩，另一种是有损压缩。在一些情况下，有损压缩也是必要的，重要的是平衡压缩比和失真率之间的关系。 所谓失真率，就是压缩前、压缩后的两串信息的差的平方。 如果信息没有任何失真，失真率是0。如果信息完全消失了，失真率是100%。 实际生活中的大量应用都是有损压缩，在兼顾了失真率的考量后，人们基本感觉不到。 通常失真率和压缩比直接相关，压缩比越大，失真率越高。采用什么样的压缩方法，压缩到何种程度，通常要看具体的应用场景。 在信息处理领域，通常不存在标准答案和最佳答案，只有针对某个场景的好答案。   10. 信息正交性 和能量不同，相同的信息使用两次，并不会产生两倍的效果。 利用多种信息消除不确定性时，所采用的信息是正交的时候，效果才最好。 如何找到正交的信息？ 首先，不同的信息要来自不同的信息源，善用不同维度的交叉信息。 其次，避免反复使用相互嵌套或者相互包含的信息。 最后，看问题要可以改变观察的角度，从不同的角度思考问题。 在选取重要且彼此尽可能正交的信息时，常用的方法是不断叠加和不断删除。不断叠加就是利用手上的信息，有效组合、排序和选择；不断删除就是不断叠加的逆向过程。   11. 互信息 相关不是因果，世界上大多数联系都是相关联系，而非因果联系。相关的联系有强有弱，若相关意义不大，我们需要寻找和利用的是强相关。 互信息是用来定量衡量相关程度的大小。 有因果关系的信息，实际上是等价的。比如A=B可以推出B=A。 没有因果关系的信息，它们之间是一种动态的相互关联的关系。比如，如果A和B比关联性比较强，我们知道A的信息后，就可以消除B的不确定性。如果A和B关联性比较弱，那这种联系就没什么意义了。 在使用互信息时，需要注意不要把两件强相关的事情的因果顺序颠倒了。   12. 信息增益 信息增益(Information Gain，IG)，在只有两个信息A和B时，IG=信息A和信息B的互信息，IG越大，说明消除的不确定性越大，A和B越具有相关性。再增加第三个信息C，它所带来的IG是在A和B的基础上增加的。以此类推，假设还有N个不同信息，它们所带来的IG，每一个都是在原来所有信息基础上递减的。这说明，率先发现和解决问题所要的信息，是增益最大的信息，越后发现的信息，带来的增益越小。 利用信息增益的概念，我们可以衡量一条信息的价值，也可以衡量一项研究发现的贡献。   13. 置信度 置信度可以简单理解为我们自己有多么确定一件事发生的概率。 在统计学上，我们一般认为，置信度不到95%的结论都是不可靠的。 提高置信度的通常办法是增加所统计样本的数量。

14. 交叉熵 交叉熵(Cross Entropy)是信息论中一个重要概念，主要用于度量两个概率分布间的差异性信息。 交叉熵讨论的是在信息误判时的损失。  

网址：信息论在生活中的应用 https://www.yuejiaxmz.com/news/view/589216

相关内容

信息技术在日常生活中的应用论文摘要怎么写
信息系统在生活中的应用
管理信息系统在生活中的应用
生活中管理信息系统的应用
试析信息管理与信息系统在企业中的应用
决策理论在生活中应用
决策理论在生活中的应用.doc
生活中的信息
情绪abc理论在生活中的应用
信息化技术在大学生公寓管理中的应用探究

随便看看