学习的西瓜皮 于 2019-03-27 15:57:42 发布前言
学算法，不得不提的就是数学归纳法。许多算法都会用到归纳假设的思想，其追溯回去便是数学归纳法。
数学归纳法
最简单和常见的数学归纳法是证明当n等于任意一个自然数时某命题成立。证明分下面两步：
证明当n = 1时命题成立。 证明如果在n = k时命题成立，那么可以推导出在n = k+1时命题也成立。（k代表任意自然数）这种方法的原理在于：首先证明在某个起点值时命题成立，然后证明从一个值到下一个值的过程有效。当这两点都已经证明，那么任意值都可以通过反复使用这个方法推导出来。把这个方法想成多米诺效应也许更容易理解一些。例如：你有一列很长的直立着的多米诺骨牌，如果你可以：
证明第一张骨牌会倒。 证明只要任意一张骨牌倒了，那么其下一张骨牌也会因为前面的骨牌倒而跟着倒。那么便可以下结论：所有的骨牌都会倒下。
应用举例
1. 前n项和
证明：S(n) = 1 + 2 + 3 …. + n 前n项和为n(n + 1) / 2
n = 1, S(1) = 1
假设n时命题成立
N+ 1时，
S（n + 1）
= S(n) + n + 1
= n(n + 1)/2 + n + 1
= (n + 1)(n + 2)/ 2
成立
2. 区域计数
问n条居一般位置的直线能将平面分成多少个区域
定义：一般位置， 任意两线不平行，任意三线不共点。
现在草稿纸上看看简单的情况，看看有没有规律。
直线 -- 区域
1 -- 2
2 -- 4
3 -- 7
4 -- 11
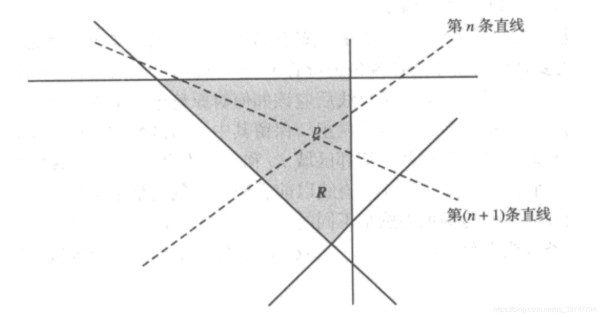
找规律 第n条直线能比n-1条直线的区域多n个
证明： 在平面内n- 1条居一般位置的直线添加一条直线会增加n个区域
n <= 3 时 显然成立
假设n-1条直线时成立
加入第n条直线
假设删去第n
