分类 数学研究 下的文章

阅读学术论文，理解研究方法和数据分析。 #生活乐趣# #阅读乐趣# #学术阅读#

证明下列级数发散或者收敛：
(1) ∑∞x=11x=1+12+13+14+...
(2) ∑∞x=11x2=1+122+132+142+...

一眼看上去，由于1/x,1/x2都会趋向零，所以它们应该是收敛的。真的是这样吗？

点击阅读全文...

今天在数学研发论坛看到了一道题目：

j=n∑j=0(jxj)=nxn+2−(n+1)xn+1+x/(x−1)2

这道题实际是求x+2x2+3x3+...+nxn的求和公式而已。

本来呢用数学归纳法是十分简单的（数学归纳法对于证明简单，对于推导就不行了），但是题目说不能用数学归纳法。只好用以下方法了。

点击阅读全文...

椭圆面积和周长的求法，看上去没有什么区别。不过实际上它们的难度有着天壤之别。

椭圆所包围的面积是S=πab，这里的a和b是半长轴和半短轴。仅根据椭圆标准方程就可以推导出来。

目前还没有找到椭圆周长的一般公式，要想精确求解，只有代入以下无穷级数：
C=2πa[1−(1/2)2(ca)2−(1⋅3/2⋅4)2c4/3a4−(1⋅3⋅5/2⋅4⋅6)2c6/5a6−...]

可以写成：
C=2πa∞∑n=0−[n∏m=1(2m−1/2m)]2c2n/a2n(2n−1)

距离c 叫做椭圆的线性离心率，等于从中心到任一焦点的距离

点击阅读全文...

在中学，有理数的定义为整数和分数的集合，统一来说就是能够写成两个整数之比的数。那相对地，无理数自然就是不能写成两个整数之比的数了，也就是无限不循环小数，比如π,√2等等。历史上无理数的发现带来了第一次数学危机，并生下了一颗“金蛋”，不过发现者却因此丢掉了生命。让我们永远铭记——希帕索斯(Hippasus)。

历史：

http://baike.baidu.com/view/1167.htm#2

在这里对无理数就不多说些什么了，主要是谈谈相关的证明而已。
先说明，以下是我自己的证明方法，当然我相信有一种方法是通用的，但是我没有找出来。

点击阅读全文...

新浪科技讯 北京时间7月28日消息，据国外媒体报道，数学经常会让聪明人感觉自己笨得不行，有时甚至会让他们很生气。

事实上，数学本身非常有趣，它是我们日常生活的一部分，每个人都能从中获得享受。只不过在课堂上，数学被一些死板的老师教死板了。以下就是英国《每日邮报》最近公布的日常生活中的趣味数学：

你身上的计算器

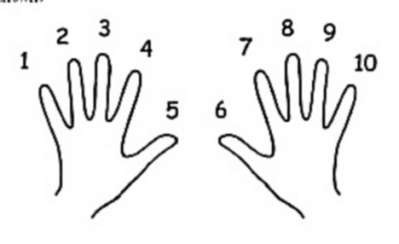
从左到右给你的手指编

点击阅读全文...

感觉题目有点像抽屉原理，不过似乎复杂一点：

有12个互不相等的自然数，它们均小于37，求证：这些自然数两两相减的差中，至少有3个相等

我的解答：

点击阅读全文...

宇宙中存在所谓的“黑洞”，只要你步入了它的视界之内，就永远也出不去了（除非你能够超光速）。在数学中，也有类似的规则，只要把一个自然数代入这个规则，都无一不会陷入无限的循环之中，这样称之为“数字黑洞”。有一个“数字黑洞”，它令人十分着迷，甚至有人称它为“企图减缓美国数学进展的阴谋”——这就是“冰雹猜想”。

冰雹猜想：
任选一个自然数。当选定的自然数是偶数，将它除以2，如是奇数，将它乘以3加上1；当变换后的自然数成了偶数，再将它除以2，如成了奇数，再将它乘以3加上1，连续进行下去，最后都“落叶归根”——变成了1。

点击阅读全文...

网址：分类 数学研究 下的文章 https://www.yuejiaxmz.com/news/view/709733

相关内容

多元文化下的勾股定理——数学文化研究性学习教学案例
调研家样本数据研究成果分享
基于机器学习方法的空气质量分类与预测研究
文章翻译学视域下林语堂《 生活的艺术》闲适风格再现研究论文
基于核心素养下的小学数学阅读实践研究
提升小学生数学学习幸福感的策略研究
研究数学，最重要是内心的平静
“生物—文化视角下的人类骨骼考古学研究——以殷墟若干遗址为例”讲座纪要—中国社会科学院考古研究所2019年度考古学研究系列学术讲座（第6讲）
数字优惠券市场现状研究分析报告
中学数学生活化”的研究性学习设计方案

随便看看