旅行商问题的回溯法求解

一旦发现食品安全问题，可以通过追溯系统快速找到问题源头并进行召回。 #生活常识# #生活安全# #食品安全追溯#

【题目】

       某售货员要到4个城市去推销商品，已知各城市之间的路程，如右图所示。

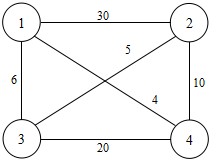
请问他应该如何选定一条从城市1出发，经过每个城市一遍，最后回到城市1的路线，使得总的周游路程最小？并分析所设计算法的计算时间复杂度。

【分析】

       该题利用回溯法求解，此时需要确定解空间的类型：我们可以知道该解空间为一棵排列树。我们假设初始的一条路线为x，x中的值为 1，2，3，……，n，表示该路线为由城市1依次经过城市2、3……到n后再回到城市1（当然是假设该路线存在）。如果不存在的话，我们只需改变一下这个排列的排列方式，再进行判断，所以可想而知，我们可以知道该解空间是一棵排列树。

       当然上述的说法，只是单纯的穷举，这并不是我们想要的回溯法，我们通过递归实现，在递归的过程中适当地“剪枝”即除去那些不可能形成最优解的解。现在我们来确定一下可行的约束条件，当我们进行递归搜索，搜索到第t层时，我们需要判断一下x[t]所代表的城市是否与上一层x[t-1]所代表的城市有“路”，如果没有的话，需要改变x[t]的值，然后继续上述判断，当出现一个满足条件的x[t]后还要判断当前从1到t-1所走的路程cc加上x[t]与x[t-1]的距离是否小于当前已经记录的最优解（最优解的初始值是一个足够大的数），如果到t的距离比当前最优解还要大的话，那么再以这条路线搜索下去的话回到城市1的路程一定比当前最优解还大，所以我们没有必要对这条路线进行下一步的搜索。最后我们来确定当搜索到叶子结点的时候我们该如何处理？已知搜索到t层时，若t = n，说明已经搜索到了叶子结点，这个时候我们还需做上述所说的两个判断，如果两个判断都通过的话，说明该解比当前最优解还优，那么我们需要将该解记录下来，并记录该解的最优值。

【伪代码】

void travel(int t) {

    if(t到达第n层即搜索到叶子结点) {

        if(城市x[t-1]可以到达城市x[t]，并且城市x[t]可以回到城市1，且此时所走的路程cc加上

            x[t-1]与x[t]的距离和x[t]与1的距离小于当前最优值bestc) {

                将最优解记录下来;

                将最优值记录下来;

            }

        return;

    }

    for(int i = t; i < n; i++) {

        if(城市x[t-1]能达到城市x[i]即这两个城市间有边，并当前所走的路程cc加上这两个城市的距离

        没有比当前最优值bestc大) {

        swap(x[i], x[t]);

        修改此时所走的路程cc;

        进入下一层递归;

        恢复原来cc的值;

        swap(x[i], x[t]);

        }

    }

}

【程序】

用C++语言编写程序，代码如下：

#include<iostream>

using namespace std;

const int INF = 10000000;

int n, cc = 0, bestc = INF;

int **g;

int *x, *bestx;

void travel(int t) {

if (t == n) {

if (g[x[t - 1]][x[t]] != INF && g[x[t]][1] != INF &&

(cc + g[x[t - 1]][x[t]] + g[x[t]][1] < bestc || bestc == INF)) {

for (int i = 0; i < n + 1; i++)

bestx[i] = x[i];

bestc = cc + g[x[t - 1]][x[t]] + g[x[t]][1];

}

return;

}

for (int i = t; i < n; i++) {

if (g[x[t - 1]][x[i]] != INF && (cc + g[x[t - 1]][x[i]] < bestc

|| bestc == INF)) {

swap(x[i], x[t]);

cc += g[x[t - 1]][x[t]];

travel(t + 1);

cc -= g[x[t - 1]][x[t]];

swap(x[i], x[t]);

}

}

}

void output() {

cout << bestc << endl;

cout << bestx[1];

for (int i = 2; i < n + 1; i++)

cout << " " << bestx[i];

cout << " " << bestx[1] << endl;

}

int main() {

n = 4;

g = new int*[n + 1];

x = new int[n + 1];

bestx = new int[n + 1];

for (int i = 0; i < n + 1; i++) {

g[i] = new int[n + 1];

x[i] = i;

for (int j = 0; j < n + 1; j++)

g[i][j] = INF;

}

g[1][2] = g[2][1] = 30;

g[1][3] = g[3][1] = 6;

g[1][4] = g[4][1] = 4;

g[2][3] = g[3][2] = 5;

g[2][4] = g[4][2] = 10;

g[3][4] = g[4][3] = 20;

travel(2);

output();

return 0;

}

该算法的时间复杂度为O(n!)。

网址：旅行商问题的回溯法求解 https://www.yuejiaxmz.com/news/view/762628

相关内容

旅行商问题
动态规划特训：旅行商问题（回溯法或记忆搜索法）
回溯算法（以解决n皇后问题为例）
旅行商问题（枚举，回溯，动态规划，贪心，分支界限）
旅行商问题+背包问题
背包问题：c++回溯法求解背包问题
MATLAB 旅行商问题（动态规划法）程序
用c语言实现旅行商问题的c
旅行商问题（动态规划方法，超级详细的）
关于旅行商问题几种常用算法的经验

随便看看