机器数中的原码、反码、补码三种形式

数码相机设置：曝光补偿原理 #生活技巧# #数码产品使用技巧# #数码产品入门#

文章目录 计算机"眼中"的数字数字的“单位”小数点的“位置”带符号的整数整数的大小 计算机"眼中"的数字

计算机内数据和指令都是由晶体管和门电路等元件完成的，对于这些元件来说，开或者关是其唯一的状态，这种状态的表现就是二进制的理念。就像黑客帝国世界中漫天飞的0和1一样,计算机世界使用的机器语言也只有0和1。而在机器语言中，当计算机想要表示一个数字时，这时就得使用机器数了，机器数所表示的真实数值称为真值。

机器数有两个特点：

符号数字化，通常机器数以最高位表示正负号，即0代表正数，1代表负数。数值的大小受字长显示，如8bit的机器，其可表示的真值数值范围为-127 ~ +127，机器数即11111111 ~ 01111111。 数字的“单位”

计算机数据常用的单位一般为以下四种：

位(bit)

位，音译为“比特”，没错，就是比特币的比特，它表示计算机内部二进制数码存储的最小单位。

如：0001是一个4位的二进制数。

字节（Byte）

字节，音译为“拜特”，字节是信息量的基本单位，一个字节可容纳8位二进制数码，即1个字节等于8个比特（1byte=8bit）。通常情况下，1个字节可以存入一个ASCII码，2个字节可以存放一个汉字国标码。

字（Word）

字是计算机中每次 作为一个整体进行处理的二进制数码。一个字通常由一个或多个字节组成。

字长（Word Length）

计算机中每个字所包含的位数称为字长,字长标志着计算机每次运算的最大精度，它是计算机性能的重要指标。通常CPU与内存之间的数据传送单位是一个字长，内存中用于指明一个存储位置的地址也经常是以字长为单位的。

小数点的“位置”

在机器数中，小数点的位置是隐含指定的。小数点的处理方式有以下两种方式：

定点（Fixed Point）数

在运算过程中，小数点的位置是始终固定不变的。

例如：

整数的表示：XXXXXX.

纯小数的表示：.XXXXXX

整数与小数表示：XXXX.XX

浮点(Floating Point)数

在运算过程中，小数点的位置可以根据实际需要来改变，但不能改变数值的大小。

例如：

123.4 = 12.34 *101 = 1.234 * 102 = 0.1234 * 103

可见，虽然浮点数中小数点的位置不同，但是数值的大小是不变的。

浮点数主要包括尾数（Mantissa）、指数（Exponent）、底数（Base）三个部分。

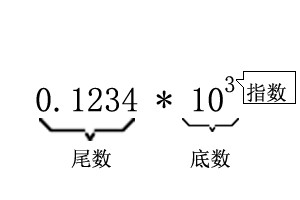
注意这里，尾数才是数值的有效部分，指数决定数值的大小，也就是说，小数点的实际位置是由指数来决定的，这也是浮点数的特性之一。

​

带符号的整数

在计算机中，一个数的正负是通过二进制数0和1去表示的。一般这个数放在一个字的最高位（Most Significant Bit），即最左边一位，记作符号位。一般带符号的整数有如下表现形式：

原码（Primitive Encoding）

原码的表示

在机器数中,如果整数的绝对值用二进制数表示，“+”、“-”符号分别用0和1去表示，这种表示方式就称为原码，记作 [x]原。其中x为真值，[x]表示真值为x的机器数，下标“原”表示该机器数为原码的表示形式。

一般来说,字长为n的原码可以定义为：

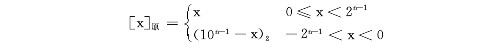
其中，真值x（整数）的表示范围是-(2n-1-1) <= x <= 2n-1-1。圆括号右侧的下标2表示其中的内容为二进制数。

原码的计算

假设字长为8，真值+3和-3用原码表示如下：

+3 = [+0000011]原 = 00000011

-3 = [-0000011]原 = 10000011

原码表示方法简单易懂，他与真值的转化，往往通过人脑就可以完成。并且原码的计算也与人类的脑力运算差不多。

例如，两个数相减，我们先要判断它们的绝对值大小，如果减数绝对值大于被减数绝对值的话要交换两者计算位置，最后求出结果后还要加上正确的符号。

补码（Complement）

模

在学习补码前我们先回忆下“模”的概念。

根据排列组合原理，一个字长为n位的字，最多能够表示出2n种不同的二进制数码。其中，数值2n 就称为该字的模(Modulo)。

用一个不是太准确但还算通俗易懂的概念解释下模。

我们有一个12小时表示法的时钟，假设现在时针指向6点钟，那么有个问题4小时前时针指向的是几点钟？

1.将时针逆时针拨动4个小时。 3 - 4 2.将时针顺时针拨动8个小时。 3 + (12 - 8) 这里只考虑这两种情况，并且两者的结果是一样的。 123

而这里的12称为“模”。

为什么要有补码？

为了简化加、减运算过程，提出了补码的概念。在介绍补码之前，先来做一个二进制计数的实验。

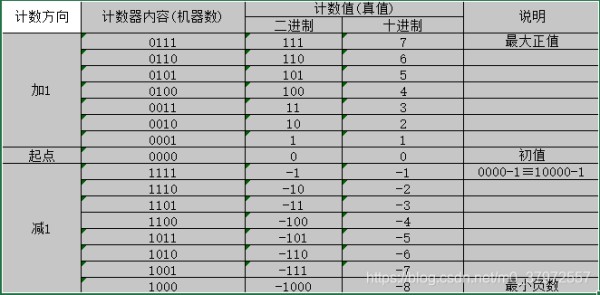
上图是一个4bit的二进制加/减计数器，我们从计数器的初始值0000开始，分别对其加1和减1计数。由上图中可见，对于数值范围为0~7的正数来说，计数器的最高有效位为0。而对于大于-8的负数来说，计数器的最高有效位为1，因此，在一定的计数范围内的计数器最高有效位的状态可以用来表示数的正负。

也就是说，其实补码在定义时，第一位不是类似原码的符号位，这里的0、1其实表示是否借位通过模的引入加减法转换为加法，恰好计算完的结果最高有效位可以来表示正负，才有了补码的符号位这一概念。

注意计数器在0000状态下减1的情况，由于不够减，实际这里已经产生了借位，这时计数器的减1结果与二进制运算10000-1的结果是等价的。因此，当计数值x小于0时，计数器的内容（机器数）实际已变成如下形式：

其中，10000B=24就是4位计数器的“模”。实际上，上图表格的内容可以通过以下补码定义方式来表示：

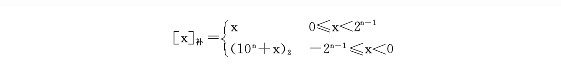
其中，n为字长，真值x(整数)的表示范围是：-2n-1 <= x <= 2n-1-1，常数（10n）2 = 2n就是该字的模。

补码的计算

同样假设字长为8，根据上面补码定义，3和-3的补码表示如下：

+3 = [+0000011]补 = 00000011

-3 = [-0000011]补 = 100000000 - 10000011 = 11111101

​

由补码的定义可知，两个互为相反数的补码满足以下关系。

[x]补 + [-x]补 = 10nB （-2n-1 <= x <= 2n-1，n为字长）

这表明[x]补与[-x]补相对模10nB（即22）是互补的。

有一种直接通过二进制数取负数补码的方法，即从二进制数的最低有效位（LSB）开始起向左，直到遇见第一个“1”为止所有数字都不变（包括这个“1”），第一个“1”以后各位数字全部取反，直到满足相应字长要求为止。

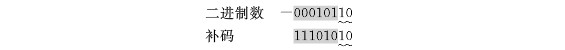
​引用上面时钟的问题，补码的引出实际将机器数的减法转换为，补码的相加。

反码（Invert Encoding）

为什么要有反码？

尽管补码可以简化加、减法运算，但是实际求补码扔需要做减法运算，为了再次优化，提出了反码的概念。利用反码直接将相加，避免了在计算补码时需要进行模的减法。

反码的定义与补码的定义类似：

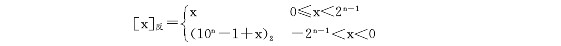
其中，n为字长，真值x（整数）的表示范围是-（2n-1 - 1） <= x <= 2n-1 - 1。

反码的计算

设字长为8，根据上面反码定义，3和-3的反码表示如下：

+3 = [+0000011]反 = 00000011

-3 = [-0000011]反 = 100000000 -1 - 0000011 = 11111111 - 00000011 = 11111100

反码定义式中

的情况。这样一个n位全为“1”的数与负数x相加的结果就是负数x逐位取反。这也是反码一词的由来。

负数的反码是有补码减1所得。

整数的大小

我们日常生活中比较两个数的大小是通过做减法来实现的，计算机也一样。

但是对于计算机来说，无符号数值的比较只需要通过是否借位来判断大小，而有符号的数值的大小比较却较为麻烦了。

首先，由于执行的是相加运算，借位状态没有任何意义了。

其次，计算过程中有可能因为溢出而无法表示正确的结果。

为了便于有符号数的大小比较，在计算机中常用“移码”来表示有符号数。所谓移码是指将有符号数x加上正偏移值B后所形成的无符号数,即

[x] 移 = B + x

其中，偏移值B为一个整数，它等于真值x最小数的绝对值。真值x的取值不能超出有符号机器数的表示范围。

字长为n的移码与补码之间的关系式：

[x] 移 = B + [x] 补 （mod 2 n）

其中，x为整数，其范围是-2n-1 <= x < 2n-1。B为一个正整数，在这里 B = |xmin| = 2n-1。下面列出了8位补码、移码与真值之间的对应关系。

真值x补码移码12701111111111111111260111111011111110………1000000011000000100000000010000000-11111111101111111………-1271000000100000001-1281000000000000000

可见这里补码最高位取反就是移码，对于计算机移码来说，最高位为1的为正数，最高位为0为负数。无论是正数还是负数，大的数的补码永远是大于小的数的，故当相同符号的数值进行比较的时候移码的大小关系和真值的大小关系一样。

网址：机器数中的原码、反码、补码三种形式 https://www.yuejiaxmz.com/news/view/859493

相关内容

数据表示——原码、反码、补码、移码
原码、反码、补码总结
计算机运算方法之（原码 补码 反码 移码）
三分钟玩转数码相机小知识
数码相机的使用方法 数码相机使用说明
单反数码相机的维护与保养
数码相机八个巧用绝招
数码相机如何使用？ 如何使用数码相机？
数码相机的正确使用攻略
回收数码产品，数码家电，数码电器，数码电子，智能数码产品

随便看看