粒子群算法优化电力系统PMU配置：基于MATLAB的IEEE30 39 57 118系统仿真验证

个性化推荐算法：基于阅读历史和兴趣的推荐系统 #生活乐趣# #阅读乐趣# #电子书推荐#

基于粒子群的PMU优化配置
软件：MATLAB
介绍：电力系统PMU优化配置，为了使电力系统达到完全可观，以PMU配置数量最少为目标函数，运用粒子群算法进行优化处理，在IEEE30 39 57 118系统进行仿真验证。
这段代码是一个使用粒子群优化算法（Particle Swarm Optimization, PSO）来解决IEEE 39节点电力系统中的PMU位置优化问题的程序。下面我将详细解释每个部分的功能和涉及的知识点。

首先，程序开始时进行了一些初始化设置，包括定义了一些参数和变量。例如，`nvar`表示变量的数量，`lb`和`ub`分别表示变量的下界和上界。`popsize`表示种群的大小，`maxiter`表示最大迭代次数。`c1`和`c2`是PSO算法中的加速常数，`damp`是阻尼因子。

接下来，程序创建了一个空的结构体数组`par`，用于存储粒子的信息。每个粒子包含三个字段：`var`表示粒子的位置（二进制向量），`fit`表示粒子的适应度值，`vel`表示粒子的速度。

然后，程序使用随机数生成算法初始化了种群中的每个粒子。对于每个粒子，它的速度被初始化为位于`lb`和`ub`之间的随机值，然后通过一个Sigmoid函数将速度转换为位置。位置的每个元素都是一个二进制值，由一个随机数和Sigmoid函数生成。

接下来，程序计算每个粒子的适应度值，即调用了一个名为`IEEE_39_Bus`的函数，并将适应度值存储在相应的字段中。

然后，程序将当前种群中的最优粒子（`bpar`）和全局最优粒子（`gpar`）初始化为第一个粒子，并记录其适应度值。

接下来是主循环部分，程序通过迭代来更新每个粒子的速度和位置。对于每个粒子，它的速度根据当前速度、个体最优位置和全局最优位置进行更新。更新公式中的随机项模拟了粒子的随机搜索行为。然后，程序对速度进行阻尼处理，以减少粒子的速度。

接下来，程序对速度进行约束处理，确保速度在`lb`和`ub`之间。

然后，程序根据新的速度更新粒子的位置，方法与初始化时类似。

接下来，程序计算每个粒子的适应度值，并将其存储在相应的字段中。

然后，程序根据新的适应度值更新个体最优位置和全局最优位置。如果某个粒子的适应度值优于个体最优位置，则更新个体最优位置。如果个体最优位置的适应度值优于全局最优位置，则更新全局最优位置。

在每次迭代结束时，程序记录全局最优适应度值。

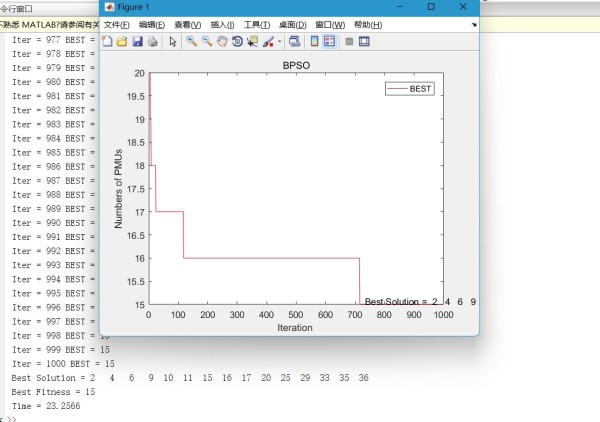
最后，程序输出结果，包括最优解的位置和适应度值，以及程序的运行时间。此外，程序还绘制了迭代次数与PMUs数量之间的关系图。

总结来说，这段代码实现了一个使用粒子群优化算法解决IEEE 39节点电力系统中PMU位置优化问题的程序。它涉及到的知识点包括粒子群优化算法、二进制编码、适应度函数的定义等。通过迭代更新粒子的位置和速度，程序寻找到最优的PMU位置，以最小化适应度函数的值。

YID:38100671997242852

电气小助手

基于粒子群算法的PMU优化配置

摘要：本文介绍了一种基于粒子群算法（Particle Swarm Optimization, PSO）的电力系统PMU位置优化配置方法。通过将PMU的数量最小化作为目标函数，并在IEEE30、39、57和118系统上进行仿真验证，本文展示了该方法的有效性和可行性。

关键词：粒子群算法，PMU优化配置，电力系统，目标函数，IEEE标准

引言
随着电力系统规模的不断扩大和复杂性的增加，对系统状态的监测和分析变得越来越重要。相位测量单元（Phasor Measurement Unit, PMU）作为一种高精度的测量设备，可以提供准确的相位和幅值信息，被广泛应用于电力系统的状态监测和故障诊断。然而，将PMU安装在系统中的每个节点上会带来高昂的成本和复杂的工程实施。因此，如何合理配置PMU的数量和位置成为一个重要的研究问题。

粒子群算法介绍
粒子群算法是一种模拟鸟群觅食行为的优化算法，通过不断迭代和搜索，寻找到问题的最优解。在粒子群算法中，每个粒子代表一个可能的解，粒子的位置和速度在搜索空间中不断更新，直到找到最优解或达到迭代次数的上限。

PMU优化配置问题建模
PMU优化配置问题可以通过目标函数的定义和约束条件的设置来进行建模。在本文中，我们将PMU的数量最小化作为目标函数，并将系统安全、故障检测和诊断等要求作为约束条件。具体地，目标函数可以定义为最小化PMU的数量，即：

minimize f(x) = sum(xi)

其中，xi为0或1，代表第i个节点是否安装PMU。

粒子群算法应用于PMU优化配置
在本文中，我们将粒子群算法应用于PMU优化配置问题。首先，我们定义了问题的参数和变量，包括变量数量、界限值、种群大小和迭代次数等。然后，我们使用随机数生成算法初始化了种群中每个粒子的位置和速度。接下来，我们根据定义的目标函数计算每个粒子的适应度值，并更新个体最优位置和全局最优位置。通过迭代更新粒子的速度和位置，我们寻找到最优的PMU配置方案。最后，我们通过输出结果和绘制关系图来评估算法的性能和效果。

仿真实验和结果分析
在本文的仿真实验中，我们选择了IEEE30、39、57和118系统作为测试案例，验证了所提出的PMU优化配置方法的有效性和可行性。通过对比不同配置方案的PMU数量和目标函数值，我们可以评估算法的性能和效果。

结论
通过将粒子群算法应用于PMU优化配置问题，本文提出了一种有效的方法来实现电力系统的完全可观测性。通过优化PMU的数量和位置，我们可以降低系统成本，提高系统的监测和分析能力。在未来的研究中，我们可以进一步改进算法的性能和效果，探索更多的优化方法和策略。

参考文献：

[1] Kennedy, J., & Eberhart, R. (1995). Particle swarm optimization. Proceedings of ICNN’95-International Conference on Neural Networks, 4, 1942-1948.
[2] Yan, Q., & Zhang, X. (2011). Optimal placement of PMUs for static and dynamic observability in power systems. IEEE Transactions on Power Systems, 26(2), 1019-1027.

【相关代码,程序地址】：http://lanzoup.cn/671997242852.html

网址：粒子群算法优化电力系统PMU配置：基于MATLAB的IEEE30 39 57 118系统仿真验证 https://www.yuejiaxmz.com/news/view/862544

相关内容

【电力系统】智能家居能源管理系统（HEMS）粒子群优化电力管理和MPC控制matlab复现
【负荷预测】基于DBO、PSO、SSA、GOOSE算法优化ELM的电力负荷预测研究附Matlab代码
基于多目标灰狼优化算法的环境经济调度研究【IEEE30节点】（Matlab实现）
【电力系统】基于分时电价条件下家庭能量管理策略研究附MATLAB代码
Matlab Simulink仿真：构建家庭能源管理系统与微电网
基于MATLAB语音识别系统GUI界面
基于java的网吧管理系统答辩PPT.pptx资源
【优化调度】基于NSGAII算法的车辆充电调度策略研究含Matlab代码
m基于遗传算法的城市生活垃圾回收网络优化matlab仿真
基于DIALux的照明优化系统设计资源

随便看看