如图.已知抛物线y=ax2+bx+c过点A.其顶点为D．(1)求抛物线的解析式,.当MB+MD的值最小时.求m的值,(3)若P是抛物线上位于直线AC上方的一个动点.求△APC的面积的最大值,(4)若抛物线的对称轴与直线AC相交于点N.E为直线AC上任意一点.过点E作EF∥ND交抛物线于点F.以N.D.E.F为顶点的四边形能否为平行四边形?若能.求点E的坐标,若不能.请说明理由． 题目和参考答案——青夏教育精英家教网——

'三分法'：将画面分为上、下、左、右四个等份，主体位于交叉点或交界线上，利于构图平衡 #生活知识# #摄影技巧# #构图原理#

分析 （1）根据待定系数法，可得答案；
（2）利用轴对称求最短路径的知识，找到B点关于直线x=1的对称点B′，连接B'D，B'D与直线x=1的交点即是点M的位置，继而求出m的值．
（3）根据平行于y轴的直线上两点间的距离是较大的纵坐标减去较小的纵坐标，可得PE的长，根据三角形的面积，可得二次函数，根据二次函数的性质，可得答案；
（4）设出点E的，分情况讨论，①当点E在线段AC上时，点F在点E上方，②当点E在线段AC（或CA）延长线上时，点F在点E下方，根据平行四边形的性质，可得关于x的方程，继而求出点E的坐标．

解答 解：（1）将A，B，C点的坐标代入解析式，得
{9a−3b+c=04a−2b+c=3c=3" role="presentation">{9a−3b+c=04a−2b+c=3c=3，
解得{a=−1b=−2c=3" role="presentation">{a=−1b=−2c=3，
抛物线的解析式为y=-x2-2x+3
（2）配方，得y=-（x+1）2+4，顶点D的坐标为（-1，4）
作B点关于直线x=1的对称点B′，如图1，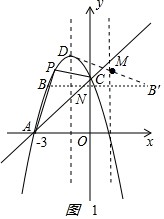
则B′（4，3），由（1）得D（-1，4），
可求出直线DB′的函数关系式为y=-15" role="presentation">15x+195" role="presentation">195，
当M（1，m）在直线DN′上时，MN+MD的值最小，
则m=-15" role="presentation">15×1+195" role="presentation">195=185" role="presentation">185．
（3）作PE⊥x轴交AC于E点，如图2，
AC的解析式为y=x+3，设P（m，-m2-2m+3），E（m，m+3），
PE=-m2-2m+3-（m+3）=-m2-3m
S△APC=12" role="presentation">12PE•|xA|=12" role="presentation">12（-m2-3m）×3=-32" role="presentation">32（m+32" role="presentation">32）2+278" role="presentation">278，
当m=-32" role="presentation">32时，△APC的面积的最大值是278" role="presentation">278；
（4）由（1）、（2）得D（-1，4），N（-1，2）
点E在直线AC上，设E（x，x+3），
①当点E在线段AC上时，点F在点E上方，则F（x，-x2-2x+3），
∵EF=DN
∴-x2-2x+3-（x+3）=4-2=2，
解得，x=-2或x=-1（舍去），
则点E的坐标为：（-2，1）．
②当点E在线段AC（或CA）延长线上时，点F在点E下方，则F（x，-x2-2x+3），
∵EF=DN，
∴（x+3）-（-x2-2x+3）=2，
解得x=−3+172" role="presentation">−3+172或x=−3−172" role="presentation">−3−172，
即点E的坐标为：（−3+172" role="presentation">−3+172，3+172" role="presentation">3+172）或（−3−172" role="presentation">−3−172，3−172" role="presentation">3−172）
综上可得满足条件的点E为E（-2，1）或：（−3+172" role="presentation">−3+172，3+172" role="presentation">3+172）或（−3−172" role="presentation">−3−172，3−172" role="presentation">3−172）．

点评 本题考查了二次函数的综合题，解（1）的关键是待定系数法，解（2）利用轴对称求最短路径；解（3）的关键是利用三角形的面积得出二次函数；解（4）的关键是平行四边形的性质得出关于x的方程，要分类讨论，以防遗漏．

网址：如图.已知抛物线y=ax2+bx+c过点A.其顶点为D．(1)求抛物线的解析式,.当MB+MD的值最小时.求m的值,(3)若P是抛物线上位于直线AC上方的一个动点.求△APC的面积的最大值,(4)若抛物线的对称轴与直线AC相交于点N.E为直线AC上任意一点.过点E作EF∥ND交抛物线于点F.以N.D.E.F为顶点的四边形能否为平行四边形?若能.求点E的坐标,若不能.请说明理由． 题目和参考答案——青夏教育精英家教网—— https://www.yuejiaxmz.com/news/view/230414

相关内容

如图.在每个小正方形的边长为1的网格中.点A.B均在格点上．(Ⅰ)线段AB的长为 ．(Ⅱ)请利用网格.用无刻度的直尺在AB上作出点P.使AP=.并简要说明你的作图方法． ． 题目和参考答案——青夏教育精英家教网——
求抛物线Y^2=2PX(P大于0）的焦点，作一直线交抛物线于A，? 爱问知识人
已知:如图.在四边形ABCD中.AB∥CD.E.F为对角线AC上两点.且AE=CF.DF∥BE．求证:四边形ABCD为平行四边形． 题目和参考答案——青夏教育精英家教网——
[题目]如图.已知AB＝12cm.CA⊥AB于点A.DB⊥AB于点B.且AC＝4cm.点P从点B向点A运动.每秒钟走1cm.点Q从点B向点D运动.每秒钟走2cm.两点同时出发.运动几秒钟后.△CPA与△PQB全等? 题目和参考答案——青夏教育精英家教网——
如图平行四边形ABCD中点EF在对角线AC上且AE=CF请你以点? 爱问知识人
“低碳生活，绿色出行”是我们倡导的一种生活方式，有关部门抽样调查了某单位员工上下班的交通方式，绘制了如下统计图： (1)填空：样本中的总人数为 人；开私家车的人数m= ；扇形统计图中“骑自行车”所在扇形的圆心角为 度； (2)补全条形统计图； (3)该单位共有2000人，积极践行这种生活方式，越来越多的人上下班由开私家车改为骑自行车．若步行，坐公交车上下——青夏教育精英家教网——
如图所示，有一固定的且内壁光滑的半球面，球心为O，最低点为C，在其内壁上有两个质量相同的小球(可视为质点)A和B，在两个高度不同的水平面内做匀速圆周运动，A球的轨迹平面高于B球的轨迹平面，A、B两球与O点的连线与竖直线OC间的夹角分别为α＝53°和β＝37°，以最低点C所在的水平面为重力势能的参考平面，则(sin37°＝，cos37°＝) A．A、B两球所受支持力的大小之比为4 ∶3 B．A、B两——青夏教育精英家教网——
“每天锻炼一小时.健康生活一辈子 .自开展“阳光体育运动 以来.学校师生的锻炼意识都增强了．某校有学生8200人.为了解学生每天的锻炼时间.学校体育组随机调查了部分学生.统计结果如表所示．表格中.m=30人, 这组数据的众数是14.5分钟,该校每天锻炼时间达到1小时的约有820人人．时间段频数频率29分钟及以下1080.5430
一质点作直线运动，已知其加速度a=2
郝强同学对建筑工地上的长臂吊车有些疑惑:不吊物体它能平衡.吊重物也能平衡.重物沿臂移动仍能平衡!后来他通过设计“移动支点式杠杆 模型弄懂了类似问题:密度及粗细都均匀的直棒AB=1.8m.放在一个宽度为40cm的凳子上.当在棒的A端固定一个铅块m铅=2kg时.棒刚好绕O1点有转动的趋势(AO1=30cm)．(1)求棒的重力G棒,(2)当在P处挂一重物时.棒刚好绕O 题目和参考答案——青夏教育精英家教网——

随便看看