智能反射面无蜂窝大规模MIMO网络容量优化方法

开启飞行模式在无信号区域可临时关闭蜂窝网络 #生活技巧# #数码产品使用技巧# #平板电脑省电技巧#

智能反射面无蜂窝大规模mimo网络容量优化方法
技术领域
1.本方法涉及无线通信领域，特别是无线通信系统的能量收集和网络容量优化。具体涉及智能反射面辅助的无蜂窝大规模mimo网络容量优化方法。

背景技术：

2.随着5g技术的发展和广泛应用，物联网技术作为一种新兴技术，广泛应用于我们生活的各个方面。由于物联网设备往往数量规模大，容易导致设备能量短缺问题，无线电力传输(wireless power transfer，wpt)被认为是解决物联网设备能源短缺问题的有效的技术。在无线供电通信网络
1.(wireless powered communication network，wpcn)中，设备首先从下行链路收集射频能量，然后通过上行链路向基站或接入点传输数据。
3.在蜂窝mimo通信网络中，多天线可以提高wpt的效率，但小区边界用户的性能仍然很差，这是由于下行wpt阶段和上行数据传输阶段的路径损耗都很大。相比较蜂窝网络，无蜂窝通信网络
2.被认为是抵抗路径损耗，提高小区边界用户性能的有效方法。具有分布式和协作特点的无蜂窝大规模mimo，被证明可以提高频谱效率和能量效率。与蜂窝大规模mimo相比，由于终端与服务接入点(access points，aps)之间的距离更小，可以避免小区边界终端的严重路径损耗。借助具有以用户为中心的架构的无蜂窝大规模mimo，[3]提出了一种无线供电的无蜂窝物联网方案，具有联合优化的下行链路和上行链路功率控制系数和并置大规模mimo相比，无蜂窝物联网的wpt效率得到了显着提高。[4]提出了一种无线供电的无蜂窝物联网网络的长期调度和功率控制方案，传感器被调度用于上行链路数据传输或下行链路功率传输，最大化所有传感器的最小时间平均可实现速率，使用李雅普诺夫优化联合确定每个时隙的传输模式和功率控制系数，提高了最小时间平均可实现速率。
[0004]
为了进一步提升无蜂窝网络的容量，需要部署更多的接入点，成本和功耗都很高。智能反射面(intelligent reflection surface，irs)是一种低成本、高能效和高增益的超表面，正在成为未来6g通信的一种有前途的智能无线电技术
[5]
。凭借大量低成本的无源元件，智能反射面能够通过调整其元件的相移，以超高的阵列增益将电磁入射信号反射到任何方向。[6]提出了智能反射面辅助的无蜂窝网络的概念，用低成本、高能效的智能反射面替代部分所需的接入点，以降低成本和功耗来提高网络容量。对于典型宽带场景中提出的智能反射面辅助无蜂窝网络，在接入点和智能反射面制定联合预编码设计问题，开发了一种交替优化算法，拉格朗日对偶变换和分数规划解耦，交替解决子问题。与传统的无小区网络相比，[6]所提出方案的网络容量可以得到显着提高。

技术实现要素：

[0005]
为克服现有技术的不足，本发明旨在提出一种针对智能反射面辅助的无蜂窝大规模mimo网络的长期调度和功率控制方法，来提升网络中最小时间平均可达速率，以提升网络容量。为此，本发明采取的技术方案是，智能反射面无蜂窝大规模mimo网络容量优化方法,建立智能反射面辅助无线供电的无蜂窝物联网模型，使用李雅普诺夫优化方法解决每
个时隙的传输模式和功率控制系数求解，利用拉格朗日对偶变换和分数规划解耦方法，交替解决复杂的非凸优化问题，实现接入点基站主动波束成形和智能反射面无源元件被动波束成形的联合优化方案。
[0006]
具体步骤如下：
[0007]
(1)建立系统模型和问题描述，方法如下：
[0008]
第一步：建立系统模型
[0009]
一个无蜂窝大规模mimo网络中，配置r个智能反射面irss，同时系统中分布着l个接入点aps和k个单天线的无线传感器用户，所有接入点都通过无损耗的回程网络与一个中心处理器cpu相连。每个智能反射面上分布着m个反射单元，并由中心处理器通过无线方式控制，其中，优化算法总的持续时间为t个时隙，对于每个时隙t，有ka个传感器处于活跃状态，传感器活跃系数：
[0010][0011]
定义传输模式符号
[0012]
δ
(t)
∈{0,1},t＝0,1,2,
…
,t
ꢀꢀ
(2)
[0013]
当δ
(t)
＝1时,传感器进行下行的无线能量转换wpt，当δ
(t)
＝0时,传感器进行上行的数据传输；
[0014]
第l个接入点和第k个传感器之间的信道，表示为从接入点到传感器的信道和接入点-智能反射面-传感器的信道的叠加，即其中表示时隙t中第r个智能反射面上的相移矩阵，约束条件
[0015][0016]
第二步：问题描述
[0017]
当δ
(t)
＝1时,传感器进行下行的无线能量转换，第k个传感器在本阶段接收到的信号可以表示为其中表示从第l个接入点到第k个传感器的波束成形向量，表示加性高斯噪声，第l个接入点发射信号的能量约束为
[0018][0019]
那么第k个传感器收集到的能量表示为：
[0020][0021]
当δ
(t)
＝0时,第l个接入点接收到的来自所有传感器的传输信号表示为
[0022][0023]
其中表示信道中的加性高斯噪声，ρu表示第k个传感器的最大发射功率，代表第k个传感器的能量控制系数，其约束条件为：
[0024][0025]
上行数据传输的信噪比表示为
[0026][0027]
那么，时隙t内第k个传感器的可达速率表示为：
[0028][0029]
第k个传感器在时隙t内用于上行数据传输的能量消耗为：
[0030][0031]
其中表示第k个传感器的电池剩余电量在时隙t的初始状态，时隙间的迭代公式为
[0032][0033]
其中，b
max
代表传感器电池的最大容量，为了确保系统正常运行，需要设定传感器正常工作电量不能低于设定值b0，即
[0034][0035]
以最大化时间平均传输速率最小的用户的速率，即
[0036][0037]
s.t.(1),(2),(3),(4),(6),(9),(11)
ꢀꢀ
(12)
[0038]
其中p(t)＝{δ
(t)
,a
(t)
,w
(t)
,ξ
(t)
,θ
(t)
}。
[0039]
(2)长期李雅普诺夫优化方法
[0040]
第一步：长期调度约束条件的构造
[0041]
p1的优化问题是一个无穷范围内的最大化最小值问题，很难直接求解。引入一个辅助变量r(t)，满足
[0042]
0≤r
(t)
≤r
max
ꢀꢀ
(13)
[0043]rmax
为当不考虑其他干扰时，所有传感器达到的最大速率，满足
[0044][0045]
并将约束(11)放宽为长期约束
[0046][0047]
定义队列和和约束(14)和(15)看做是上述两个队列是长期稳定的，即
[0048][0049][0050]
那么，问题p1可以重新写为
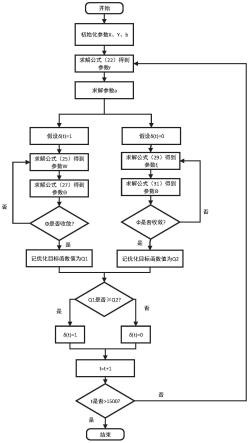
[0051][0052]
s.t.(1),(2),(3),(4),(6),(9),(13),(16),(17)
ꢀꢀ
(18)
[0053]
第二步：李雅普诺夫问题的求解
[0054]
定义二次李雅普诺夫函数以及李雅普诺夫漂移变量δ(t)＝l(t+1)-l(t)。当漂移达到最小值时，队列将更趋向于达到最稳定的状态，由于长期调度约束(16)和(17)，优化问题p2可以被视为最大化和保持队列稳定之间的权衡，即
[0055][0056]
其中w是预设的权衡系数，根据李雅普诺夫函数的性质，经过简单放缩变换，得到优化目标函数：
[0057][0058]
优化问题写为：
[0059]
[0060]
s.t.(1),(2),(3),(4),(6),(9),(13)
ꢀꢀ
(21)
[0061]
(3)分时隙的联合交替优化策略
[0062]
第一步：求解r
(t)
[0063][0064]
第二步：求解δ
(t)
[0065]
分时隙进行第四步联合求解，分δ(t)＝1和δ(t)＝0两种情况分别得到目标函数值q1和q2，选择函数值较大的一种情况进行选择；
[0066]
第三步：求解a
(t)
[0067]
当δ(t)＝1时，将xk(t)最大的ka个传感器的状态设为1，其余设为0；当δ(t)＝0时，将yk(t)最大的ka个传感器的状态设为1，其余设为0；
[0068]
第四步：联合求解w
(t)
,ξ
(t)
,θ
(t)
[0069]
假设δ(t)＝1，优化问题p3写为
[0070][0071][0072][0073]
这是一个包含w
(t)
和θ
(t)
两个变量的非凸问题，可以通过固定一个变量求解另一个变量的方法求解。
[0074]
a)固定θ
(t)
求解w
(t)
[0075][0076]
其中由于函数g1(w
(t)
)对于w
(t)
是非凸的，用一次泰勒展开
[4]
近似求解：
[0077][0078][0079]
其中
[0080]
b)固定w
(t)
求解θ
(t)
[0081]
定义辅助变量θ
(t)
＝θ
(t)1rm
，那么θ
(t)
＝diag(θ
(t)
)，求解θ
(t)
然后可以直接得到θ
(t)
，目标函数
[0082][0083]
化为关于θ
(t)
的非凸函数，用一次泰勒展开
[4]
近似求解：
[0084][0085][0086]
对两个变量分别固定一个求解另一个，交替进行，并得到每次优化变量的值，不断迭代直到的值保持收敛，并记录为q1；
[0087]
优化问题p3写为
[0088][0089][0090][0091][0092]
这是一个包含ξ
(t)
和θ
(t)
两个变量的非凸问题，通过固定一个变量求解另一个变量的方法求解：
[0093]
a)固定θ
(t)
求解ξ
(t)
[0094]
优化问题写成
[0095][0096][0097][0098]
[0099]
其中对于变量ξ
(t)
，使用拉格朗日变换，添加辅助变量将函数g3(ξ
(t)
)从对数中解耦，得到一个典型的分数规划问题，利用分数规划进行求解；
[0100]
b)固定ξ
(t)
求解θ
(t)
[0101]
优化问题
[0102][0103]
其中采用分数规划方法，并使用辅助变量θ
(t)
＝θ
(t)1rm
，将问题转化为求解一个qcqp问题：
[0104][0105][0106]
使用matlab中的cvx工具箱求解θ
(t)
，并进一步解出θ
(t)
；
[0107]
对两个变量分别固定一个求解另一个，交替进行，并得到每次优化变量的值，不断迭代直到的值保持收敛，并记录为q2。
[0108]
详细步骤如下：
[0109]
第一步：初始化xk(0)＝0,yk(0)＝0，b
k(0)
＝b0；
[0110]
第二步：根据公式(22)求解r
(t)
；
[0111]
第三步：根据xk(t)和yk(t)分别求解a
(t)
，记为a
x(t)
和a
y(t)
；
[0112]
第四步：a)假设δ(t)＝1，初始化θ
0(t)
，
[0113]
b)固定θ
(t)
，根据公式(25)求解w
(t)
，
[0114]
c)固定w
(t)
，根据公式(27)求解θ
(t)
，
[0115]
d)循环迭代b)和c)，直到的值保持收敛，记录为q1；
[0116]
第五步：a)假设δ(t)＝0，初始化θ
0(t)
，
[0117]
b)固定θ
(t)
，根据公式(29)求解ξ
(t)
，
[0118]
c)固定ξ
(t)
，根据公式(31)求解θ
(t)
，
[0119]
d)循环迭代b)和c)，直到的值保持收敛，记录为q2；
[0120]
第六步：若q1≥q2，δ(t)＝1，否则δ(t)＝0；
[0121]
第七步：t＝t+1，返回第二步。
[0122]
本发明的特点及有益效果是：
[0123]
1.通过对本发明的仿真实验，得到的系统最小时间平均可达速率相较[4]中的方案有了较大提升，如图3所示。
[0124]
2.本发明实现了所有传感器时间平均剩余电量的基本稳定，且基本高于预设最小
工作电量，如图4所示。
附图说明：
[0125]
图1系统模型。
[0126]
图2信道模型。
[0127]
图3仿真实验，得到的系统最小时间平均收效示意图。
[0128]
图4实现所有传感器时间平均剩余电量的基本稳定效果示意图。
[0129]
图5本发明流程图。
具体实施方式
[0130]
本发明提出了一种针对智能反射面辅助的无蜂窝大规模mimo网络的长期调度和功率控制方法，来提升网络中最小时间平均可达速率，以提升网络容量。本发明在无蜂窝大规模mimo网络容量优化算法的基础上，结合智能反射面和无蜂窝大规模mimo网络的特点，在李雅普诺夫优化算法的基础上，对网络中接入点的波束成形和传感器的能量控制算法进行改进，创新点主要有：
[0131]
(1)为了进一步提升无蜂窝大规模mimo的网络容量，本发明在无线供电的无蜂窝物联网方案基础上提出了智能反射面辅助无线供电的无蜂窝物联网模型，使用李雅普诺夫优化方法解决每个时隙的传输模式和功率控制系数求解，进一步提高最小时间平均可实现速率；
[0132]
(2)利用拉格朗日对偶变换和分数规划解耦方法，交替解决复杂的非凸优化问题，实现接入点基站主动波束成形和智能反射面无源元件被动波束成形的联合优化方案。
[0133]
本发明在无线供电的无蜂窝物联网方案基础上提出了一种针对智能反射面辅助的无蜂窝大规模mimo网络的长期调度和功率控制方法，包括下列步骤：
[0134]
(1)建立系统模型和问题描述，方法如下：
[0135]
第一步：建立系统模型
[0136]
一个无蜂窝大规模mimo网络中，配置r个智能反射面(intelligent reflection surface，irss)，同时系统中分布着l个接入点(accessible points，aps)和k个单天线的无线传感器用户，如图1所示。所有接入点都通过无损耗的回程网络与一个具有无限算力的中心处理器(central processing unit，cpu)相连。每个智能反射面上分布着m个反射单元，并由中心处理器通过无线方式控制。
[0137]
假设优化算法总的持续时间为t个时隙，对于每个时隙t，有ka个传感器处于活跃状态，传感器活跃系数
[0138][0139]
定义传输模式符号
[0140]
δ
(t)
∈{0,1},t＝0,1,2,
…
,t
ꢀꢀ
(33)
[0141]
当δ
(t)
＝1时,传感器进行下行的无线能量转换(wireless power transfer,wpt)，当δ
(t)
＝0时,传感器进行上行的数据传输。
[0142]
如图2所示,第l个接入点和第k个传感器之间的信道，可以表示为从接入点到传感
器的信道和接入点-智能反射面-传感器的信道的叠加，即其中表示时隙t中第r个智能反射面上的相移矩阵，约束条件
[0143][0144]
第二步：问题描述
[0145]
当δ
(t)
＝1时,传感器进行下行的无线能量转换。第k个传感器在本阶段接收到的信号可以表示为其中表示从第l个接入点到第k个传感器的波束成形向量，表示加性高斯噪声。第l个接入点发射信号的能量约束为
[0146][0147]
那么第k个传感器收集到的能量可以表示为
[0148][0149]
当δ
(t)
＝0时,第l个接入点接收到的来自所有传感器的传输信号可以表示为
[0150][0151]
其中表示信道中的加性高斯噪声，ρu表示第k个传感器的最大发射功率，代表第k个传感器的能量控制系数，其约束条件为
[0152][0153]
上行数据传输的信噪比可以表示为
[0154][0155]
那么，时隙t内第k个传感器的可达速率可以表示为
[0156][0157]
第k个传感器在时隙t内用于上行数据传输的能量消耗为
[0158][0159]
其中表示第k个传感器的电池剩余电量在时隙t的初始状态，时隙间的迭代公式为
[0160][0161]
其中，b
max
代表传感器电池的最大容量。为了确保系统正常运行，需要设定传感器正常工作电量不能低于设定值b0，即
[0162][0163]
在无蜂窝网络中最大化最小用户速率是有意义的
2.。本发明考虑了一个长期优化问题，以最大化时间平均传输速率最小的用户的速率，即
[0164][0165]
s.t.(1),(2),(3),(4),(6),(9),(11)
ꢀꢀ
(43)
[0166]
其中p(t)＝{δ
(t)
,a
(t)
,w
(t)
,ξ
(t)
,θ
(t)
}。
[0167]
(2)长期李雅普诺夫优化方法
[0168]
第一步：长期调度约束条件的构造
[0169]
p1的优化问题是一个无穷范围内的最大化最小值问题，很难直接求解。引入一个辅助变量r(t)，满足
[0170]
0≤r
(t)
≤r
max
ꢀꢀ
(44)
[0171]rmax
为当不考虑其他干扰时，假设所有传感器可以达到的最大速率，满足
[0172][0173]
并将约束(11)放宽为长期约束
[0174][0175]
定义队列和和约束(14)和(15)可以看做是上述两个队列是长期稳定的，即
[0176][0177][0178]
那么，问题p1可以重新写为
[0179][0180]
s.t.(1),(2),(3),(4),(6),(9),(13),(16),(17)
ꢀꢀ
(49)
[0181]
第二步：李雅普诺夫问题的求解
[0182]
定义二次李雅普诺夫函数以及李雅普诺夫漂移变量
δ(t)＝l(t+1)-l(t)。当漂移达到最小值时，队列将更趋向于达到最稳定的状态。由于长期调度约束(16)和(17)，优化问题p2可以被视为最大化和保持队列稳定之间的权衡，即
[0183][0184]
其中w是预设的权衡系数。根据李雅普诺夫函数的性质，经过简单放缩变换，得到优化目标函数
[0185][0186]
优化问题可以写为
[0187][0188]
s.t.(1),(2),(3),(4),(6),(9),(13)
ꢀꢀ
(52)
[0189]
(3)分时隙的联合交替优化策略
[0190]
第一步：求解
[0191][0192]
第二步：求解δ
(t)
[0193]
分时隙进行第四步联合求解，分δ(t)＝1和δ(t)＝0两种情况分别得到目标函数值q1和q2，选择函数值较大的一种情况进行选择。
[0194]
第三步：求解a
(t)
[0195]
当δ(t)＝1时，将xk(t)最大的ka个传感器的状态设为1，其余设为0；当δ(t)＝0时，将yk(t)最大的ka个传感器的状态设为1，其余设为0。
[0196]
第四步：联合求解w
(t)
,ξ
(t)
,θ
(t)
[0197]
假设δ(t)＝1，优化问题p3可以写为
[0198][0199][0200]
[0201]
这是一个包含w
(t)
和θ
(t)
两个变量的非凸问题，可以通过固定一个变量求解另一个变量的方法求解。
[0202]
c)固定θ
(t)
求解w
(t)
[0203][0204]
其中由于函数g1(w
(t)
)对于w
(t)
是非凸的，可以用一次泰勒展开
[4]
近似求解：
[0205][0206][0207]
其中
[0208]
d)固定w
(t)
求解θ
(t)
[0209]
定义辅助变量θ
(t)
＝θ
(t)1rm
，那么θ
(t)
＝diag(θ
(t)
)。求解θ
(t)
然后可以直接得到θ
(t)
。目标函数
[0210][0211]
可以化为关于θ
(t)
的非凸函数，用一次泰勒展开
[4]
近似求解：
[0212][0213][0214]
对两个变量分别固定一个求解另一个，交替进行，并得到每次优化变量的值，不断迭代直到的值保持收敛，并记录为q1。
[0215]
假设δ(t)＝0，优化问题p3可以写为
[0216]
[0217][0218][0219][0220]
这是一个包含ξ
(t)
和θ
(t)
两个变量的非凸问题，可以通过固定一个变量求解另一个变量的方法求解。
[0221]
a)固定θ
(t)
求解ξ
(t)
[0222]
优化问题可以写成
[0223][0224][0225][0226][0227]
其中对于变量ξ
(t)
，这是一个典型的分数规划问题，利用分数规划
[7]-[8]
进行求解。具体可以使用拉格朗日变换
[6]
，添加辅助变量将函数g3(ξ
(t)
)从对数中解耦，得到一个典型的分数规划问题，利用分数规划
[7]-[8]
进行求解；
[0228]
b)固定ξ
(t)
求解θ
(t)
[0229]
优化问题
[0230][0231]
其中采用分数规划方法
[7]-[8]
，并使用辅助变量θ
(t)
＝θ
(t)1rm
，将问题转化为求解一个qcqp问题：
[0232][0233][0234]
可以使用matlab中的cvx工具箱求解θ
(t)
，并进一步解出θ
(t)
。
[0235]
对两个变量分别固定一个求解另一个，交替进行，并得到每次优化变量的值，不断迭代直到的值保持收敛，并记录为q2。
[0236]
本发明的一个实例具体步骤如下：
systems—part ii:uplink scheduling via matching,"ieee transactions on signal processing,vol.66,no.10,pp.2631
–
2644,2018。

网址：智能反射面无蜂窝大规模MIMO网络容量优化方法 https://www.yuejiaxmz.com/news/view/628034

相关内容

【网优】浅谈LTE无线网络优化
无线网络优化设计方案模板.doc
5G无线网络规划与优化
移动通信网络规划与优化的一课一得
蜂窝物联网
无线网络优化课程心得
5G网络优化的意义
《无线网络优化》
连接数突破 40 亿大关，全球蜂窝物联网模组行业梳理 2024 年云栖大会召开：2024 年云栖大会于 9 月 19 日至 21 日召开，吸引了大模型、自动驾驶、机器人等领域...
无线网络优化体系

随便看看