原理:
重要性采样主要用于难以直接采样的数据分布上,采样是指从已知的某个分布采样一些数据进行后续运算,但是数据分布比较复杂不容易进行采样,针对这种问题使用蒙特卡罗法,例如:
复杂的概率密度函数p(x),求解随机变量基于此概率下的某个数学期望,根据蒙特卡罗法转换为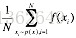
虽然p(x)比较复杂,但是我们可以对上面的公式进行一些变换,使用常见的分布采样,复杂的采样分布为p(x),另一个简单的可采样且定义域与p(x)相同的概率密度函数q(x),因此可以得到:
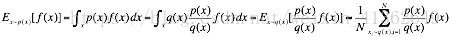
代码:
#encoding=utf-8 """ created on 2018-08-12 @author wt Description:重要性采样表示从某一个分布获取某些数据,并利用这些数据完成更多的运算 当某一个密度函数很复杂的时候可以采用近似他的分布代替它 """ import numpy as np import math """x服从的分布""" def gaussian(x,u,sigma): return math.exp(-(x-u)**2/(2*sigma*sigma))/math.sqrt(2*math.pi*sigma*sigma) def importance_sampling(sigma,sample_sigma): """作用相当于取f(x)""" origin = [] for i in range(100000): a = np.random.normal(1.0,sigma) origin.append(a) sample = [] for i in range(100000): """计算f(x)的值""" fx = np.random.normal(1.0,sample_sigma) """原始复杂分布为px,现找同分布的q(x)来代替""" qx = gaussian(a,1.0,sample_sigma) px = gaussian(a,1.0,sigma) sample.append(fx*px/qx) origin = np.array(origin) sample = np.array(sample) print(np.mean(origin),np.std(origin)) print(np.mean(sample),np.std(sample)) importance_sampling(1.0,1.0) importance_sampling(1.0,0.5) importance_sampling(1.0,2) xs = np.linspace(-10,10,101) y1 = [gaussian(x,1.0,1.0) for x in xs] y2 = [gaussian(x,1.0,0.5) for x in xs] y3 = [gaussian(x,1.0,2) for x in xs] import matplotlib.pyplot as plt fig = plt.figure(figsize=(8,5)) plt.plot(xs,y1,label='sigma=1.0') plt.plot(xs,y2,label='sigma=0.5',linestyle=':') plt.plot(xs,y3,label='sigma=2.0',linestyle='--') plt.legend() plt.show() 结果:



