逻辑回归实现与应用

遇到冲突，用事实和逻辑而非情绪回应。 #生活技巧# #沟通技巧# #网络沟通#

文章目录

介绍Sigmoid分布函数逻辑回归模型对数损失函数梯度下降法逻辑回归实现 加载数据函数代码汇总逻辑回归逻辑回归 scikit-learn 实现

介绍

逻辑回归（Logistic Regression），又叫逻辑斯蒂回归，是机器学习中一种十分基础的分类方法，由于算法简单而高效，在实际场景中得到了广泛的应用。本次实验中，我们将探索逻辑回归的原理及算法实现，并使用 scikit-learn 构建逻辑回归分类预测模型。

因为今天要解决的是一个二分类问题，所以先介绍此函数

python实现：

def sigmoid(z):

sigmoid = 1 / (1 + np.exp(-z))

return sigmoid

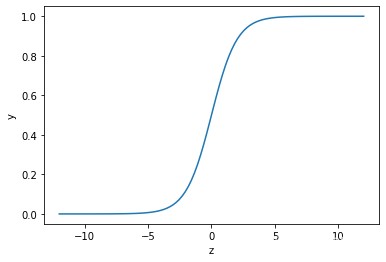
这个图像呈现出完美的 S 型（Sigmoid 的含义）。它的取值仅介于 0 00 和 1 11 之间，且关于 z = 0 z=0z=0 轴中心对称。同时当 z zz 越大时，y yy 越接近于 1 11，而 z zz 越小时，y yy 越接近于 0 00。如果我们以 0.5 0.50.5 为分界点，将 > 0.5 >0.5>0.5 或 < 0.5 <0.5<0.5 的值分为两类，这不就是解决 0 − 1 0-10−1 二分类问题的完美选择嘛。

逻辑回归模型

如果一组连续随机变量符合 Sigmoid 函数样本分布，就称作为逻辑分布。逻辑分布是概率论中的定理，是一种连续型的概率分布。
在逻辑回归中，定义：

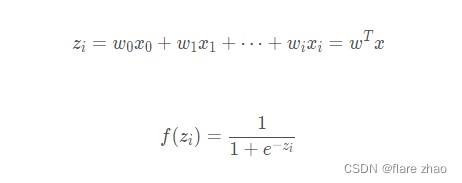
即：
​

由于目标值 y yy 只有 0 和 1 两个值，那么如果记 y = 1 y=1y=1 的概率为 h w ( x ) h_{w}(x)hw​(x)，则此时 y = 0 y=0y=0 的概率为 1 − h w ( x ) 1-h_{w}(x)1−hw​(x)。那么，我们可以记作逻辑回归模型条件概率分布：

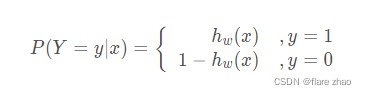
其可等价写为似然函数：
 

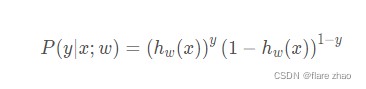
对于 i ii 个样本的总概率而言实际上可以看作单样本概率的乘积，记为 L ( w ) L(w)L(w)：
 

由于连乘表示起来非常复杂，我们应用数学技巧，即两边取对数将连乘转换为连加的形式，即：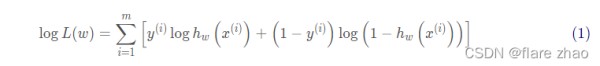

对数损失函数

函数(1)衡量了事件发生的总概率。根据最大似然估计原理，只需要通过对 () 求最大值，即得到 的估计值。而在机器学习问题中，我们需要一个损失函数，并通过求其最小值来进行参数优化。所以，对数似然函数取负数就可以被作为逻辑回归的对数损失函数：

python实现:

def loss(h, y):

loss = (-y * np.log(h) - (1 - y) * np.log(1 - h)).mean()

return loss

梯度下降法

之前我已经写过一期梯度下降法相关的blog，名为【机器学习】梯度下降法求解线性回归参数，但是其中对于数学原理的介绍并不是很详尽，这次我将结合上述本次公式对梯度下降法再次讲解，其实梯度的概念是高等数学中的内容，很明显重点就是求导，因为我们想知道的是如何下降最快，这样只需要沿着上升最快的反方向走就可以了，也就是沿着梯度的反向走，按照步长一点一点走，不然就有可能跳过最小值。

梯度是一个向量，它表示某一函数在该点处的方向导数沿着该方向取得最大值，即函数在该点处沿着该方向（此梯度的方向）变化最快，变化率最大（为该梯度的模）。简而言之，对于一元函数而言，梯度就是指在某一点的导数。而对于多元函数而言，梯度就是指在某一点的偏导数组成的向量。

我们先针对公式（1）化简：

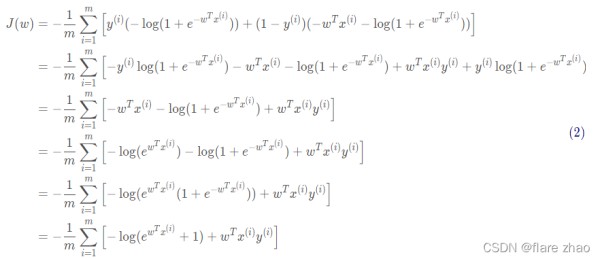
接下来，我们针对公式（2）求导：
 

即：
 

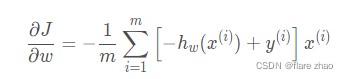
向量的形式表达为：
 

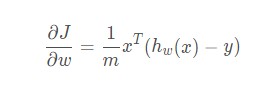
当我们得到梯度的方向，然后乘以一个常数 α \alphaα，就可以得到每次梯度下降的步长(上图箭头的长度)。最后，通过多次迭代，找到梯度变化很小的点，也就对应着损失函数的极小值了。其中，常数 α \alphaα 往往也被称之为学习率 Learning Rate。执行权重更新的过程为：

def gradient(X, h, y):

gradient = np.dot(X.T, (h - y)) / y.shape[0]

return gradient

逻辑回归实现

加载数据

import pandas as pd

import matplotlib.pyplot as plt

import numpy as np

df = pd.read_csv(

"https://labfile.oss.aliyuncs.com/courses/1081/course-8-data.csv", header=0) # 加载数据集

df.head() # 预览前 5 行数据

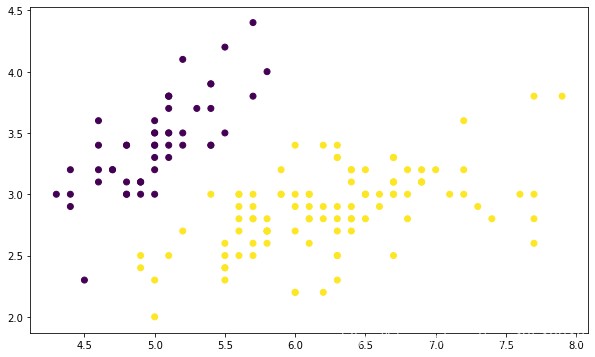
函数代码汇总

def sigmoid(z):

# Sigmoid 分布函数

sigmoid = 1 / (1 + np.exp(-z))

return sigmoid

def loss(h, y):

# 损失函数

loss = (-y * np.log(h) - (1 - y) * np.log(1 - h)).mean()

return loss

def gradient(X, h, y):

# 梯度计算

gradient = np.dot(X.T, (h - y)) / y.shape[0]

return gradient

def Logistic_Regression(x, y, lr, num_iter):

# 逻辑回归过程

intercept = np.ones((x.shape[0], 1)) # 初始化截距为 1

x = np.concatenate((intercept, x), axis=1)

w = np.zeros(x.shape[1]) # 初始化参数为 0

for i in range(num_iter): # 梯度下降迭代

z = np.dot(x, w) # 线性函数

h = sigmoid(z) # sigmoid 函数

g = gradient(x, h, y) # 计算梯度

w -= lr * g # 通过学习率 lr 计算步长并执行梯度下降

l = loss(h, y) # 计算损失函数值

return l, w # 返回迭代后的梯度和参数

逻辑回归

x = df[['X0', 'X1']].values

y = df['Y'].values

lr = 0.01 # 学习率

num_iter = 30000 # 迭代次数

# 训练

L = Logistic_Regression(x, y, lr, num_iter)

L

逻辑回归 scikit-learn 实现

LogisticRegression(penalty='l2', dual=False, tol=0.0001, C=1.0, fit_intercept=True, intercept_scaling=1, class_weight=None, random_state=None, solver='liblinear', max_iter=100, multi_class='ovr', verbose=0, warm_start=False, n_jobs=1)

介绍其中几个常用的参数，其余使用默认即可：

penalty: 惩罚项，默认为 L 2 L_{2}L2​ 范数。dual: 对偶化，默认为 False。tol: 数据解算精度。fit_intercept: 默认为 True，计算截距项。random_state: 随机数发生器。max_iter: 最大迭代次数，默认为 100。

另外，solver 参数用于指定求解损失函数的方法。默认为 liblinear（0.22 开始默认为
lbfgs），适合于小数据集。除此之外，还有适合多分类问题的 newton-cg, sag, saga 和 lbfgs
求解器。这些方法都来自于一些学术论文，有兴趣可以自行搜索了解。

from sklearn.linear_model import LogisticRegression

model = LogisticRegression(tol=0.001, max_iter=10000, solver='liblinear') # 设置数据解算精度和迭代次数

model.fit(x, y)

model.coef_, model.intercept_

文章来源：【机器学习】逻辑回归实现与应用_ccql's Blog-CSDN博客_逻辑回归方法应用 

网址：逻辑回归实现与应用 https://www.yuejiaxmz.com/news/view/717799

相关内容

Python实现简单算法乘法：提升编程效率与逻辑思维
论古希腊逻辑方法对生活世界的回应
逻辑推理：归纳法和演绎法
新的课程标准：学习逻辑=生活逻辑+学科逻辑？
真正的高手，相信逻辑而不是现实 人类日常生活中常用的两种基本逻辑方式：一种是归纳法；另一种是演绎法。归纳法是人类最基础、最常见的用智形式，这是一种内置在...
简单的逻辑学【全本
逻辑决策在生活中的应用
严密的逻辑=横向逻辑+纵向逻辑+金字塔结构
大师说：设计的底层逻辑是“回归生活 以人为本”
司法裁判中法官如何应用经验法则和逻辑规则

随便看看