【有作图代码】自由能原理：大脑与信息论的“节能专家”，一个优化系统状态的“智慧策略”

发布时间：2025-02-21 05:06

安装智能家居系统，自动优化充电策略 #生活常识# #环保节能技巧# #电动汽车推广#

【有作图代码】自由能原理：大脑与信息论的“节能专家”，一个优化系统状态的“智慧策略”

第一节：自由能原理与节能专家的类比与核心概念【尽可能通俗】

自由能原理就像是一个“节能专家”，在大脑和信息论中扮演着优化系统状态的角色。它帮助大脑高效地处理信息，减少不必要的能耗，同时确保系统状态的稳定与优化。
这就像是一个精明的家庭主妇在管理家庭开支，既要保证生活质量，又要尽可能地节省开支。

在信息论中，自由能则是一个衡量通信或信号处理系统效率的指标，它关乎如何最有效地传递信息。而大脑功能中的自由能原理，则是大脑如何优化其内部状态，以最小化与外界环境的差异，实现高效的信息处理。

第二节：自由能原理与信息论自由能的核心概念与应用

2.1 核心概念核心概念定义比喻或解释自由能原理（大脑）大脑通过最小化自由能（即预测误差与内部状态复杂度的和）来优化其功能与结构。像是大脑在“精打细算”，确保信息处理既准确又高效。自由能（信息论）在通信或信号处理中，自由能通常与熵或不确定性相关，用于衡量系统的效率或信息的传递成本。像是信息传输中的“能耗指标”，越低表示效率越高。 2.2 应用场景领域应用描述大脑功能解释大脑如何根据外部输入调整内部状态，实现学习、记忆、决策等功能。信息论与通信优化信号编码、解码过程，提高信息传输的效率和可靠性。 2.3 与节能的类比

自由能原理在大脑中的应用就像是一个家庭在努力节能减排，既要保证生活的舒适度（准确性），又要尽可能地降低能耗（复杂度）。
在信息论中，则像是优化通信线路，减少信号损失，提高传输效率。

第三节：公式探索与推演运算

3.1 自由能原理的基本形式（大脑）

自由能原理可以表示为：

F = − log ⁡ P ( s ∣ m ) + D K L [ Q ( s ∣ m ) ∣ ∣ P ( s ∣ m ) ] F = - \log P(s|m) + D_{KL}[Q(s|m)||P(s|m)] F=−logP(s∣m)+DKL[Q(s∣m)∣∣P(s∣m)]

其中， F F F 表示自由能， P ( s ∣ m ) P(s|m) P(s∣m) 表示在给定模型 m m m 下状态 s s s 的概率， D K L D_{KL} DKL 表示Kullback-Leibler散度，用于衡量两个分布之间的差异， Q ( s ∣ m ) Q(s|m) Q(s∣m) 表示大脑对状态 s s s 的预测分布。

3.2 自由能在信息论中的表达

在信息论中，自由能可能与熵或互信息相关，例如：

H ( X ) = − ∑ P ( x ) log ⁡ P ( x ) H(X) = - \sum P(x) \log P(x) H(X)=−∑P(x)logP(x)

其中， H ( X ) H(X) H(X) 表示随机变量 X X X的熵，衡量了 $ X X X 的不确定性或信息量。

3.3 公式推演与比对

虽然大脑功能中的自由能原理与信息论中的自由能概念在形式上有所不同，但它们都体现了优化系统状态、减少不确定性的思想。在大脑功能中，自由能的最小化意味着大脑在努力减少预测误差和内部状态的复杂度；而在信息论中，自由能（如熵）的最小化则意味着信息的有效传递和接收。

第四节：相似公式比对

公式/原理共同点不同点自由能原理（大脑）优化系统状态，减少不确定性。专注于大脑功能，涉及预测误差和内部状态复杂度的最小化。熵（信息论）衡量系统的不确定性或信息量。广泛应用于通信、信号处理等领域，不涉及大脑功能的具体机制。互信息（信息论）衡量两个随机变量之间的依赖关系。更侧重于信息之间的关联，而不是系统状态的优化。

第五节：核心代码与可视化

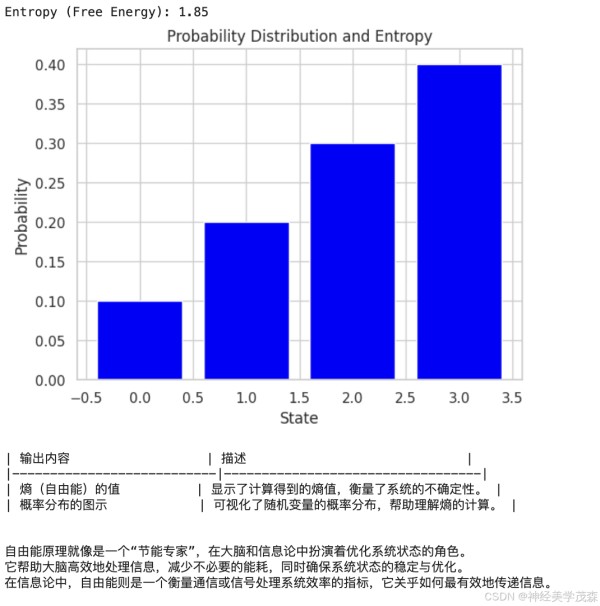
由于自由能原理涉及复杂的数学计算和理论推导，这里我们提供一个简化的Python代码示例，用于演示如何计算自由能（在信息论中的熵）并可视化其变化。请注意，这只是一个示意性的代码，并不直接对应于大脑功能中的自由能原理。

import numpy as np import matplotlib.pyplot as plt import seaborn as sns # 定义随机变量的概率分布 probabilities = np.array([0.1, 0.2, 0.3, 0.4]) # 计算熵（自由能的一种形式） entropy = -np.sum(probabilities * np.log2(probabilities)) # 打印熵的值 print(f"Entropy (Free Energy): {entropy:.2f}") # 可视化概率分布 sns.set_theme(style="whitegrid") plt.bar(range(len(probabilities)), probabilities, color='blue') plt.xlabel('State') plt.ylabel('Probability') plt.title('Probability Distribution and Entropy') plt.show() # 打印详细的输出信息 print(""" | 输出内容 | 描述 | |---------------------------|----------------------------------| | 熵（自由能）的值 | 显示了计算得到的熵值，衡量了系统的不确定性。 | | 概率分布的图示 | 可视化了随机变量的概率分布，帮助理解熵的计算。 | """) print(""" 自由能原理就像是一个“节能专家”，在大脑和信息论中扮演着优化系统状态的角色。它帮助大脑高效地处理信息，减少不必要的能耗，同时确保系统状态的稳定与优化。在信息论中，自由能则是一个衡量通信或信号处理系统效率的指标，它关乎如何最有效地传递信息。 """) 12345678910111213141516171819202122232425262728293031323334

在这里插入图片描述

输出内容描述熵（自由能）的值显示了计算得到的熵值，衡量了系统的不确定性。概率分布的图示可视化了随机变量的概率分布，帮助理解熵的计算。

参考文献

Friston, K. (2010). The free-energy principle: a unified brain theory? Nature Reviews Neuroscience, 11(2), 127-138.Cover, T. M., & Thomas, J. A. (2006). Elements of Information Theory. Wiley-Interscience.

参考文献内容概述：

Friston的论文提出了自由能原理，作为理解大脑功能与状态的理论框架，强调了大脑通过最小化自由能来实现内部状态与外部环境的动态平衡。Cover和Thomas的著作《Elements of Information Theory》是信息论领域的经典教材，详细阐述了熵、互信息等概念及其在通信和信号处理中的应用。